题目内容
5.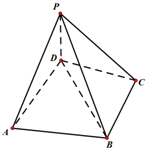 如图,四棱锥P-ABCD中,底面ABCD为四边形,△ABD是边长为2的正三角形,BC⊥CD,BC=CD,PD⊥AB,平面PBD⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为四边形,△ABD是边长为2的正三角形,BC⊥CD,BC=CD,PD⊥AB,平面PBD⊥平面ABCD.(Ⅰ)求证:PD⊥平面ABCD;
(Ⅱ)若二面角C-PB-D的平面角的余弦值为$\frac{\sqrt{6}}{6}$,求PD的长.
分析 (Ⅰ)连AC交BD于点O,由平面几何知识易知AC⊥BD,又平面ABCD⊥平面PBD,利用线面面面垂直的判定与性质定理即可得出.
(Ⅱ)如图,以O 为坐标原点,OC 为x 轴,OD 为y 轴,建立如图空间直角坐标系,利用平面的法向量的夹角即可得出.
解答 (Ⅰ)证明:连AC交BD于点O,由平面几何知识易知AC⊥BD,
又平面ABCD⊥平面PBD,BD 是交线,AC?平面ABCD,
∴AC⊥平面PBD,又PD?平面PBD,
∴AC⊥PD,又PD⊥AB,AC∩AB=A,
∴PD⊥平面ABCD.
(Ⅱ)解:如图,以O 为坐标原点,OC 为x 轴,OD 为y 轴,
建立如图空间直角坐标系,
设PD=a,则C(1,0,0),D(0,1,0),B(0,-1,0),
P(0,1,a),
易知$\overrightarrow{n_1}=(1,0,0)$ 是平面PBD 的一个法向量,
$\overrightarrow{BC}=(1,1,0),\overrightarrow{BP}=(0,2,a)$,
设$\overrightarrow{n_2}=(x,y,z)$ 是平面PBC 的一个法向量,则$\left\{\begin{array}{l}{\overrightarrow{{n}_{2}}•\overrightarrow{BC}=0}\\{\overrightarrow{{n}_{2}}•\overrightarrow{BP}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{x+y=0}\\{2y+az=0}\end{array}\right.$,取 $\overrightarrow{n_2}=(a,-a,2)$,
∴$cosθ=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|\overrightarrow{n_1}|•|\overrightarrow{n_2}|}}=\frac{a}{{1•\sqrt{2{a^2}+4}}}=\frac{{\sqrt{6}}}{6}$.
解得:a=1,∴PD 的长为1.
点评 本题考查了线面面面垂直的判定与性质定理、平面的法向量的夹角、数量积运算性质、向量夹角公式,考查了空间想象能力、推理能力与计算能力,属于中档题.

| 晚上 | 白天 | 总计 | |
| 男婴 | 45 | B | |
| 女婴 | A | 47 | C |
| 总计 | 98 | D | 180 |

则a81的位置是( )
| A. | 第13行第2个数 | B. | 第14行第3个数 | C. | 第13行第3个数 | D. | 第17行第2个数 |
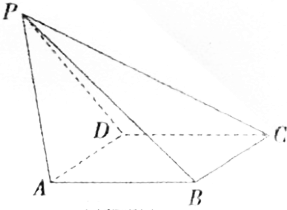 如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BDA=60°.
如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BDA=60°.