题目内容
10.下列函数中,y的最小值为2的是( )| A. | y=x+$\frac{1}{x}$ | B. | y=x2+$\frac{1}{x^2}$ | C. | y=lgx+$\frac{1}{lgx}$ | D. | y=sinx+$\frac{1}{sinx}$ | ||||
| E. | y=x2+$\frac{1}{x^2}$ |
分析 利用基本不等式的性质.
解答 解:由基本不等式的性质$a+b≥2\sqrt{ab}$(a>0,b>0)
y=$x+\frac{1}{x}$,当x>0时,y≥2,当x<0时,y≤-2,∴A不对;
lgx+$\frac{1}{lgx}$中,当lgx>0时,y≥2,当lgx<0时,y≤-2,∴C不对;
同理,sinx+$\frac{1}{sinx}$中,当sinx>0时,y≥2,sinx<0时,y≤-2,∴D不对;
y=x2+$\frac{1}{x^2}$,∵${x}^{2}>0,\frac{1}{{x}^{2}}>0$,∴${x}^{2}+\frac{1}{{x}^{2}}≥2\sqrt{1}$成立,∴B对.
故选B.
点评 本题考查了基本不等式性质的利用,注意基本不等式的性质$a+b≥2\sqrt{ab}$中的a>0,b>0.如果无法确定,需要分正,负考虑.

练习册系列答案
相关题目
1.已知函数f(x)=loga(-x2+log2ax)对任意x∈(0,$\frac{1}{2}$)都有意义,则实数a的取值范围是( )
| A. | [$\frac{1}{128}$,$\frac{1}{2}$) | B. | [$\frac{1}{64}$,$\frac{1}{2}$) | C. | [$\frac{1}{32}$,$\frac{1}{2}$) | D. | [$\frac{1}{16}$,$\frac{1}{2}$) |
5.直线x+y+1=0的倾斜角和斜率分别是( )
| A. | 45°,1 | B. | 135°,-1 | C. | 45°,-1 | D. | 90°,不存在 |
19.已知从球的一内接长方体的一个顶点出发的三条棱长分别为3,4,5,则此球的表面积为( )
| A. | 25π | B. | 50π | C. | 125π | D. | 均不正确 |
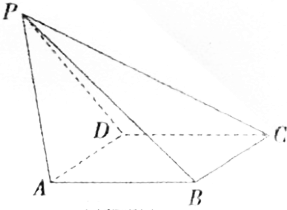 如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BDA=60°.
如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BDA=60°.