题目内容
下列命题中为真命题的是（ ）
| A、?x∈R，x2+1＜0 |
| B、?x∈Z，3x+1是整数 |
| C、?x∈R，|x|＞3 |
| D、?x∈Q，x2∈Z |
考点：全称命题,特称命题
专题：简易逻辑
分析：直接利用特称命题与全称命题的真假判断选项即可．
解答：
解：?x∈R，x2+1＜0，显然不成立；
?x∈Z，3x+1是整数，正确；
?x∈R，|x|＞3，x=0不成立，所以C错误．
?x∈Q，x2∈Z，例如x=
，则x2∉Z，D错误．
故选：B．
?x∈Z，3x+1是整数，正确；
?x∈R，|x|＞3，x=0不成立，所以C错误．
?x∈Q，x2∈Z，例如x=
| 1 |
| 2 |
故选：B．
点评：本题考查全称命题与特称命题的真假的判断，反例法的应用．
练习册系列答案
相关题目
若书架上放有的数学，物理，化学书分别是5本，3本，2本，则随机抽出一本是物理书的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若 x＞0，y＞0，且x+y=s，xy=p，则下列命题中正确的是（ ）
A、当且仅当x=y时s有最小值2
| ||
B、当且仅当x=y时p有最大值
| ||
C、当且仅当p为定值时s有最小值2
| ||
D、若s为定值，当且仅当x=y时p有最大值
|
已知α是第一象限角，那么
是（ ）
| α |
| 2 |
| A、第一象限角 |
| B、第二象限角 |
| C、第一或第二象限角 |
| D、第一或第三象限角 |
已知奇函数f（x）在[-1，0]上为单调递减函数，又α、β为锐角三角形两内角且α＞β，则下列结论正确的是（ ）
| A、f（cos α）＞f（cos β） |
| B、f（sin α）＞f（sin β） |
| C、f（sin α）＞f（cos β） |
| D、f（sin α）＜f（cos β） |
经过点（0，-2）且在两坐标轴上截距和为2的直线方程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
圆心在直线x=2上的圆C与y轴交于两点A（0，-4），B（0，-2），则圆C的方程为（ ）
| A、（x-2）2+（y-3）2=5 |
| B、（x-2）2+（y-3）2=25 |
| C、（x-2）2+（y+3）2=5 |
| D、（x-2）2+（y+3）2=25 |
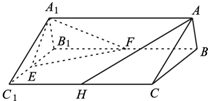如图，在直三棱柱ABC-A1B1C1中，AB=AC=1，AA1=2，E、F分别是棱B1C1、B1B的中点，H在棱CC1上，且AB⊥AH．