题目内容
设向量
、
分别对应复数z1、z2，若
⊥
，则
是（ ）
| OZ1 |
| OZ2 |
| OZ1 |
| OZ2 |
| z2 |
| z1 |
| A、非负数 | B、纯虚数 |
| C、正实数 | D、不确定 |
考点：复数的基本概念
专题：数系的扩充和复数
分析：设Z1（a，b），Z2（c，d），由于
⊥
，可得ac+bd=0．再利用复数的运算法则即可得出．
| OZ1 |
| OZ2 |
解答：
解：设Z1（a，b），Z2（c，d），
∵
⊥
，∴ac+bd=0．
∴
=
=
=
=
i，
若ad-bc=0时为实数，否则为纯虚数．
故选：D．
∵
| OZ1 |
| OZ2 |
∴
| z2 |
| z1 |
| c+di |
| a+bi |
| (c+di)(a-bi) |
| (a+bi)(a-bi) |
| ac+bd+(ad-bc)i |
| a2+b2 |
| ad-bc |
| a2+b2 |
若ad-bc=0时为实数，否则为纯虚数．
故选：D．
点评：本题考查了复数的运算法则和有关概念，属于基础题．
练习册系列答案
相关题目
如图中的直线l1，l2，l3的斜率分别为k1，k2，k3，则（ ）
| A、k1＜k3＜k2 |
| B、k3＜k2＜k1 |
| C、k3＜k1＜k2 |
| D、k1＜k2＜k3 |
如图中阴影部分表示的集合是（ ）
| A、B∩CUA |
| B、A∩（CUB） |
| C、CU（A∩B） |
| D、CU（A∪B） |
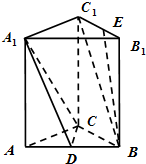如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=BB1，点D是AB的中点，