题目内容
已知复数z1满足(z1-2)(1+i)=1-i(i为虚数单位),复数z2的虚部为2,
(Ⅰ)若z1•z2是实数,求z2;
(Ⅱ)若z1•z2是纯虚数,求z2.
(Ⅰ)若z1•z2是实数,求z2;
(Ⅱ)若z1•z2是纯虚数,求z2.
考点:复数代数形式的乘除运算,复数的基本概念
专题:数系的扩充和复数
分析:由已知求得复数z1,设出复数z2,利用复数的乘法运算得到z1•z2.
(Ⅰ)由z1•z2的虚部等于0求z2;
(Ⅱ)由z1•z2的实部等于0且虚部不等于0求z2.
(Ⅰ)由z1•z2的虚部等于0求z2;
(Ⅱ)由z1•z2的实部等于0且虚部不等于0求z2.
解答:
解:由(z1-2)(1+i)=1-i,得
z1=
+2=
+2=
+2=2-i.
设z2=a+2i,则z1•z2=(2-i)(a+2i)=(2a+2)+(4-a)i.
(Ⅰ)由z1•z2是实数,得4-a=0,a=4,则z2=4+2i;
(Ⅱ)由z1•z2是纯虚数,得2a+2=0,a=-2,则z2=-2+2i;
z1=
| 1-i |
| 1+i |
| (1-i)2 |
| (1+i)(1-i) |
| -2i |
| 2 |
设z2=a+2i,则z1•z2=(2-i)(a+2i)=(2a+2)+(4-a)i.
(Ⅰ)由z1•z2是实数,得4-a=0,a=4,则z2=4+2i;
(Ⅱ)由z1•z2是纯虚数,得2a+2=0,a=-2,则z2=-2+2i;
点评:本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
已知a>1,函数y=a|x2-x-2|的图象与函数y=|logax|的图象的交点个数是( )
| A、0 | B、1 | C、2 | D、3 |
如图中的直线l1,l2,l3的斜率分别为k1,k2,k3,则( )


| A、k1<k3<k2 |
| B、k3<k2<k1 |
| C、k3<k1<k2 |
| D、k1<k2<k3 |
如图中阴影部分表示的集合是( )


| A、B∩CUA |
| B、A∩(CUB) |
| C、CU(A∩B) |
| D、CU(A∪B) |
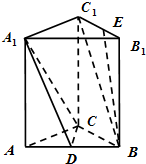 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=BB1,点D是AB的中点,
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=BB1,点D是AB的中点,