题目内容
已知函数f(x)=blnx-ax+1(ab>0)
(1)讨论f(x)在其定义域上的单调性.
(2)若b=1时,f(x)≤0恒成立,求实数a的取值范围.
(1)讨论f(x)在其定义域上的单调性.
(2)若b=1时,f(x)≤0恒成立,求实数a的取值范围.
考点:利用导数研究函数的单调性,函数恒成立问题
专题:综合题,导数的综合应用
分析:(1)求导数,利用导数的正负,结合函数的定义域可得函数的单调区间;
(2)b=1时,f(x)≤0恒成立,即lnx-ax+1≤0恒成立,即a≥
恒成立,求出y=
的最大值,即可求出实数a的取值范围.
(2)b=1时,f(x)≤0恒成立,即lnx-ax+1≤0恒成立,即a≥
| lnx+1 |
| x |
| lnx+1 |
| x |
解答:
解:(1)∵f(x)=blnx-ax+1(ab>0),
∴f′(x)=
-a=
,
当a>0,b>0时,由f′(x)>0,结合函数的定义域可得函数的单调增区间为(0,
);
由f′(x)<0,结合函数的定义域可得函数的单调减区间为(
,+∞);
当a<0,b<0时,由f′(x)>0,结合函数的定义域可得函数的单调增区间为(
,+∞);
由f′(x)<0,结合函数的定义域可得函数的单调减区间为(0,
);
(2)b=1时,f(x)≤0恒成立,即lnx-ax+1≤0恒成立,即a≥
恒成立,
设y=
,则y′=
,
∴函数y=
在(0,1)上单调递增,在(1,+∞)上单调递减,
∴x=1时,y=
的最大值为1,
∴a≥1.
∴f′(x)=
| b |
| x |
| b-ax |
| x |
当a>0,b>0时,由f′(x)>0,结合函数的定义域可得函数的单调增区间为(0,
| b |
| a |
由f′(x)<0,结合函数的定义域可得函数的单调减区间为(
| b |
| a |
当a<0,b<0时,由f′(x)>0,结合函数的定义域可得函数的单调增区间为(
| b |
| a |
由f′(x)<0,结合函数的定义域可得函数的单调减区间为(0,
| b |
| a |
(2)b=1时,f(x)≤0恒成立,即lnx-ax+1≤0恒成立,即a≥
| lnx+1 |
| x |
设y=
| lnx+1 |
| x |
| -lnx |
| x2 |
∴函数y=
| lnx+1 |
| x |
∴x=1时,y=
| lnx+1 |
| x |
∴a≥1.
点评:本题考查求实数a的取值范围,考查利用导数研究函数的单调性,考查恒成立求参数的取值范围问题.恒成立求参数的取值范围问题是近几年高考中出现频率相当高的一类型题,它比较全面的考查了导数的应用,突出了导数的工具性作用.

练习册系列答案
相关题目
在直角坐标系中,方程(x+y-1)(
-y)=0所表示的曲线为( )
| 3+2x-x2 |
| A、一条直线和一个圆 |
| B、一条线段和一个圆 |
| C、一条直线和半个圆 |
| D、一条线段和半个圆 |
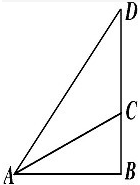 已知某建筑公司在高出地面20m的小山顶建造了一座电视台CD,如图所示,设B为电视塔的正下方水平面上的点,在坡脚取一点A测得∠CAD=45°,∠CAB=α,且tanα=
已知某建筑公司在高出地面20m的小山顶建造了一座电视台CD,如图所示,设B为电视塔的正下方水平面上的点,在坡脚取一点A测得∠CAD=45°,∠CAB=α,且tanα=