题目内容
11.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点F1的直线l交椭圆于A、B两点,|AB|的最小值为3,且△ABF2的周长为8.(Ⅰ)求椭圆的方程;
(Ⅱ)点A关于x轴的对称点为A′,直线A′B交x轴于点M,求△ABM面积的取值范围.
分析 (I)把x=-c代入椭圆的方程可得:解得y=$±\frac{{b}^{2}}{a}$.当AB⊥x轴时,弦长|AB|取得最小值$\frac{2{b}^{2}}{a}$=3.根据△ABF2的周长为8,可得4a=8.又$c=\sqrt{{a}^{2}-{b}^{2}}$,联立解出即可得出.
(II)设A(x1,y1),B(x2,y2),A′(x1,-y1).直线AB的方程为my=x+1,与椭圆方程联立化为:(3m2+4)y2-6my-9=0,利用根与系数的关系可得:|AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$,直线A′B的方程为:y+y1=$\frac{{y}_{2}+{y}_{1}}{{x}_{2}-{x}_{1}}$=(x-x1),令y=0,可得:xM=$\frac{{y}_{1}{x}_{2}+{y}_{2}{x}_{1}}{{y}_{2}+{y}_{1}}$=-4.M(-4,0).利用点到直线的距离公式可得:点M到直线AB的距离d,利用S△ABM=$\frac{1}{2}d|AB|$及其利用导数研究函数的单调性极值与最值、不等式的性质即可得出.
解答 解:(I)把x=-c代入椭圆的方程可得:y2=${b}^{2}(1-\frac{{c}^{2}}{{a}^{2}})$,解得y=$±\frac{{b}^{2}}{a}$.
当AB⊥x轴时,弦长|AB|取得最小值$\frac{2{b}^{2}}{a}$=3.
∵△ABF2的周长为8,∴4a=8.
又$c=\sqrt{{a}^{2}-{b}^{2}}$,联立解得a=2,b=$\sqrt{3}$,c=1.
∴椭圆的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(II)设A(x1,y1),B(x2,y2),A′(x1,-y1).
直线AB的方程为my=x+1,
联立$\left\{\begin{array}{l}{my=x+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,化为:(3m2+4)y2-6my-9=0,
∴y1+y2=$\frac{6m}{3{m}^{2}+4}$,y1y2=$\frac{-9}{3{m}^{2}+4}$.
|AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$\frac{12(1+{m}^{2})}{4+3{m}^{2}}$
直线A′B的方程为:y+y1=$\frac{{y}_{2}+{y}_{1}}{{x}_{2}-{x}_{1}}$=(x-x1),
令y=0,可得:xM=$\frac{{y}_{1}{x}_{2}+{y}_{2}{x}_{1}}{{y}_{2}+{y}_{1}}$=$\frac{{y}_{1}(m{y}_{2}-1)+{y}_{2}(m{y}_{1}-1)}{{y}_{2}+{y}_{1}}$=$\frac{2m{y}_{1}{y}_{2}}{{y}_{2}+{y}_{1}}$-1=-4.
∴M(-4,0).
点M到直线AB的距离d=$\frac{|-4+1|}{\sqrt{{m}^{2}+1}}$=$\frac{3}{\sqrt{{m}^{2}+1}}$.
∴S△ABM=$\frac{1}{2}d|AB|$=$\frac{1}{2}×$$\frac{3}{\sqrt{{m}^{2}+1}}$×$\frac{12(1+{m}^{2})}{4+3{m}^{2}}$=18×$\frac{\sqrt{1+{m}^{2}}}{3{m}^{2}+4}$=$\frac{18}{3\sqrt{{m}^{2}+1}+\frac{1}{\sqrt{{m}^{2}+1}}}$.(m2>0).
令$\sqrt{{m}^{2}+1}$>1,g(t)=3t+$\frac{1}{t}$,g′(t)=3-$\frac{1}{{t}^{2}}$=$\frac{3{t}^{2}-1}{{t}^{2}}$>0,因此函数g(t)在(1,+∞)上单调递增,∴g(t)>4.
∴S△ABM∈$(0,\frac{9}{2})$.
∴△ABM面积的取值范围是$(0,\frac{9}{2})$.
点评 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、弦长公式、点到直线的距离公式、不等式的性质、利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案| A. | $\frac{1}{{2}^{8}eln2}$ | B. | $\frac{1}{{2}^{9}}$ | C. | $\frac{e}{{2}^{8}ln2}$ | D. | $\frac{e}{{2}^{9}}$ |
| A. | $\frac{7}{3}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | 4 |
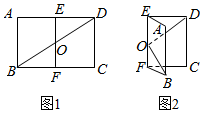 如图1,已知矩形ABCD中,AB=2,AD=2$\sqrt{2}$,E,F分别是AD,BC的中点,对角线BD与EF交于O点,沿EF将矩形ABFE折起,使平面ABFE与平面EFCD所成角为60°.在图2中:
如图1,已知矩形ABCD中,AB=2,AD=2$\sqrt{2}$,E,F分别是AD,BC的中点,对角线BD与EF交于O点,沿EF将矩形ABFE折起,使平面ABFE与平面EFCD所成角为60°.在图2中: