题目内容

6．设2134与1455的最大公约数为m，则m化为三进制数为10121（3）．

分析 利用“辗转相除法”、进位制方法即可得出．

解答 解：2134=1455+679，1455=679×2+97，679=97×7，
∴2134与1455的最大公约数为97，∴m=97．
用97连续除3取余数，可得：97化为三进制数=10121（3）．
故答案为：10121（3）．

点评 本题考查了“辗转相除法”、进位制方法，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
16．在正三棱柱（底面是正三角形的直棱柱）ABC-A1B1C1中，AB=AA1=2．若点M在△ABC所在平面上运动，且使得△AC1M的面积为1，则动点M的轨迹为（　　）
A．圆B．椭圆C．双曲线D．抛物线
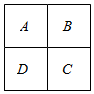17．用五种不同的颜色来涂如图所示的田字形区域，要求同一区域上用同一种颜色，相邻区域用不同的颜色（A与C、B与D不相邻）．
（1）求恰好使用两种颜色完成涂色任务的概率；
（2）设甲、乙两人各自相互独立完成涂色任务，记他们所用颜色的种数差的绝对值为ξ，求ξ的分布列及数学期望E（ξ）
14．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，2），则$\overrightarrow{a}$•（$\overrightarrow{a}$-$\overrightarrow{b}$）=4．
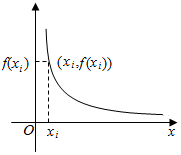1．已知函数f（x）=$\frac{1}{x}$（x＞0），对于正数x1，x2，…，xn（n∈N+），记Sn=x1+x2+…+xn，如图，由点（0，0），（xi，0），（xi，f（xi）），（0，f（xi））构成的矩形的周长为Ci（i=1，2，…，n），都满足Ci=4Si（i=1，2，…，n）．
（Ⅰ）求x1；
（Ⅱ）猜想xn的表达式（用n表示），并用数学归纳法证明．
11．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1、F2，过点F1的直线l交椭圆于A、B两点，|AB|的最小值为3，且△ABF2的周长为8．
（Ⅰ）求椭圆的方程；
（Ⅱ）点A关于x轴的对称点为A′，直线A′B交x轴于点M，求△ABM面积的取值范围．
18．用数学归纳法证明：当n≥2，n∈N时，$\frac{1}{n}$+$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{{n}^{2}}$＞1．
15．如图1，在直角梯形ABCD中，AB∥CD，AB⊥AD，且AE=1，AB=2，CD=3，E，F分别为AB，CD上得点，以EF为轴将正方形ADFE向上翻折，使平面ADFE与平面BEFC垂直．如图2．
（1）若点P在线段BD上，使得FP⊥平面BDC，求FP的长；
（2）求多面体AEBDFC的体积．
15．在△ABC中，角A，B，C所对的边分别为a，b，c，若sin（A+B）=$\frac{1}{3}$，a=3，c=4，则sinA=（　　）
A．$\frac{2}{3}$B．$\frac{1}{4}$C．$\frac{3}{4}$D．$\frac{1}{6}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网