题目内容
2.点P是线段AB上的一个动点,AB=a,在AB同侧以AP、PB为边分别作等边△APM和△BPN,求线段MN的中点Q的轨迹.分析 分别延长AM、BN交于点H,易证四边形MPNH为平行四边形,得出G为PH中点,则G的运行轨迹为三角形HAB的中位线.
解答  解:如图,分别延长AM、BN交于点H
解:如图,分别延长AM、BN交于点H
∵∠A=∠NPB=60°
∴AH∥PN,
∵∠B=∠MPA=60°,
∴BH∥PM,
∴四边形MPNH为平行四边形,
∴MN与HP互相平分.
∵G为MN的中点,
∴G也正好为PH中点,
即在P的运动过程中,G始终为PH的中点,
∴G的运行轨迹为三角形HAB的中位线.
点评 本题考查了三角形中位线定理及等边三角形的性质,解答本题的关键是作出辅助线,找到点G移动的规律,判断出其运动路径,综合性较强.

练习册系列答案
相关题目
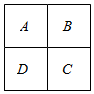 用五种不同的颜色来涂如图所示的田字形区域,要求同一区域上用同一种颜色,相邻区域用不同的颜色(A与C、B与D不相邻).
用五种不同的颜色来涂如图所示的田字形区域,要求同一区域上用同一种颜色,相邻区域用不同的颜色(A与C、B与D不相邻).