题目内容
20.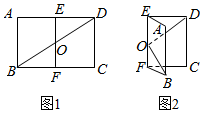 如图1,已知矩形ABCD中,AB=2,AD=2$\sqrt{2}$,E,F分别是AD,BC的中点,对角线BD与EF交于O点,沿EF将矩形ABFE折起,使平面ABFE与平面EFCD所成角为60°.在图2中:
如图1,已知矩形ABCD中,AB=2,AD=2$\sqrt{2}$,E,F分别是AD,BC的中点,对角线BD与EF交于O点,沿EF将矩形ABFE折起,使平面ABFE与平面EFCD所成角为60°.在图2中:(1)求证:BO⊥DO;
(2)求平面DOB分割三棱柱AED-BFC所得上部分的体积.
分析 (1)利用勾股定理分别求出OD,OB,BD,利用勾股定理的逆定理即可证出结论;
(2)截面上部分是一个四棱锥D-ABOE,底面为直角梯形,高为底面等边三角形的高.
解答 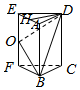 (1)证明:∵BF$\stackrel{∥}{=}$DE,∴△OED≌△OFB,
(1)证明:∵BF$\stackrel{∥}{=}$DE,∴△OED≌△OFB,
∴OE=OF=$\frac{1}{2}$AB=1,OD=OB=$\frac{1}{2}$BD=$\frac{1}{2}$$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{3}$,连结BC,BD,
∵EF⊥BF,EF⊥CF,∴∠BFC为平面ABFE与平面EFCD所成角,
∴∠BFC=60°,又BF=BC,
∴△BFC是等边三角形,∴BC=BF=$\sqrt{2}$,
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{6}$.
∴OD2+OB2=BD2,
∴BO⊥DO.
(2)解:取AE的中点H,连结DH,则DH⊥平面ABFE,且DH=$\frac{\sqrt{3}}{2}AE$=$\frac{\sqrt{6}}{2}$.
∴VD-ABOE=$\frac{1}{3}$S梯形ABOE•DH=$\frac{1}{3}×\frac{1}{2}×(1+2)×\sqrt{2}×\frac{\sqrt{6}}{2}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查了棱柱的结构特征,二面角的定义,棱锥的体积计算,属于基础题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
10.已知甲在上班途中要经过两个路口,在第一个路口遇到红灯的概率为0.5,两个路口连续遇到红灯的概率为0.4,则甲在第一个路口遇到红灯的条件下,第二个路口遇到红灯的概率为( )
| A. | 0.6 | B. | 0.7 | C. | 0.8 | D. | 0.9 |
12.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=5,则2$\overrightarrow{a}$-$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
8.执行如图的程序框图,若程序运行中输出的一组数是(x,-12),则x的值为( )


| A. | 27 | B. | 81 | C. | 243 | D. | 729 |


 某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.
某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.