题目内容
16.当实数x,y满足$\left\{\begin{array}{l}{x+2y-4≤0}\\{x-y-1≤0}\\{x≥1}\end{array}\right.$时,ax+y≤4恒成立,则实数a的取值范围是(-∞,$\frac{3}{2}$].分析 由约束条件作出可行域,再由ax+y≤4恒成立,结合可行域内特殊点A,B,C的坐标满足不等式列不等式组,求解不等式组得实数a的取值范围.
解答 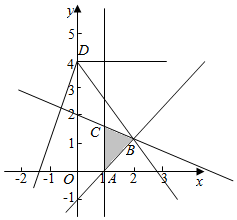 解:由约束条件作可行域如图
解:由约束条件作可行域如图
联立 $\left\{\begin{array}{l}{x=1}\\{x+2y-4=0}\end{array}\right.$,解得C(1,$\frac{3}{2}$ ).
联立 $\left\{\begin{array}{l}{x-y-1=0}\\{x+2y-4=0}\end{array}\right.$,解得B(2,1).
在x-y-1=0中取y=0得A(1,0).
由ax+y≤4得y≤-ax+4
要使ax+y≤4恒成立,
则平面区域在直线y=-ax+4的下方,
若a=0,则不等式等价为y≤4,此时满足条件,
若-a>0,即a<0,平面区域满足条件,
若-a<0,即a>0时,要使平面区域在直线y=-ax+4的下方,
则只要B在直线的下方即可,
即2a+1≤4,得0<a≤$\frac{3}{2}$.
综上a≤$\frac{3}{2}$
∴实数a的取值范围是(-∞,$\frac{3}{2}$].
故答案为:(-∞,$\frac{3}{2}$].
点评 本题考查线性规划,考查了数形结合的解题思想方法,考查了数学转化思想方法,训练了不等式组得解法,是中档题.

练习册系列答案
相关题目
6.两枚均匀的骰子一起投掷,记事件A={至少有一枚骰子6点向上},B={两枚骰子都是6点向上},则P(B|A)=( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{36}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{11}$ |
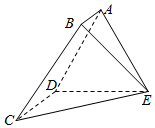 如图,在空间多面体ABCDE中,四边形ABCD为直角梯形,AB∥DC,AD⊥CD,△ADE是正三角形,CD=DE=2AB=2a,CE=$\sqrt{2}$CD.
如图,在空间多面体ABCDE中,四边形ABCD为直角梯形,AB∥DC,AD⊥CD,△ADE是正三角形,CD=DE=2AB=2a,CE=$\sqrt{2}$CD.
