题目内容
10.已知圆(x-a)2+y2=4截直线y=x-4所得的弦的长度为$2\sqrt{2}$,则a=2或6.分析 先求出圆心(a,0)到直线y=x-4的距离d=$\frac{|a-4|}{\sqrt{2}}$,再由勾股定理能求出a.
解答 解:∵圆(x-a)2+y2=4截直线y=x-4所得的弦的长度为$2\sqrt{2}$,
圆心(a,0)到直线y=x-4的距离d=$\frac{|a-4|}{\sqrt{2}}$,
∴$\sqrt{4-(\frac{|a-4|}{\sqrt{2}})^{2}}$=$\sqrt{2}$,
解得a=2或a=6.
故答案为:2或6.
点评 本题考查实数值的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
18.已知点A(1,-2,2),B(2,-2,-1),C(6,5,2),O为坐标原点,则三棱锥O-ABC的体积为( )
| A. | $\frac{65}{3}$ | B. | $\frac{\sqrt{65}}{3}$ | C. | $\frac{\sqrt{65}}{6}$ | D. | $\frac{65}{6}$ |
5.设有算法如图所示:如果输入A=225,B=135,则输出的结果是( )
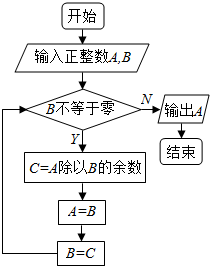

| A. | 90 | B. | 45 | C. | 2 | D. | 0 |
15.已知椭圆$\frac{x^2}{2}$+y2=1与直线y=x+m交于A、B两点,且|AB|=$\frac{4\sqrt{2}}{3}$,则实数m的值为( )
| A. | ±1 | B. | ±$\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | ±$\sqrt{2}$ |
19.如图的程序框图表示算法的运行结果是( )


| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
20.已知抛物线x2=8y上的点P到抛物线的焦点距离为5,则点P的纵坐标为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |