Question

12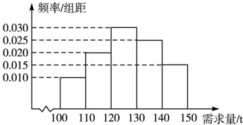．经销商经销某种农产品，在一个销售季度内，每售出1t该产品获利润500元，未售出的产品，每1t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130t该农产品．以X（单位：t，100≤X≤150）表示下一个销售季度内的市场需求量，T（单位：元）表示下一个销售季度内经销该农产品的利润．
（I）将T表示为X的函数；
（II）根据直方图求利润T不少于57 000元的频率；
（Ⅲ）在直方图的需求量分组中，以各组的区间中点值代表该组的各个值 （例如：若需求量X∈[100，110），则取X=105），估计T的平均值．

Answer 1

分析 （Ⅰ）由题意先分段写出，当x∈[100，130）和x∈[130，150）时的利润值，利用分段函数写出即可；
（Ⅱ）由（I）知，利润T不少于57000元，当且仅当120≤x≤150，再由直方图知需求量X∈[120，150]的频率为0.7，由此估计得出结论；
（Ⅲ）利用利润T的数学期望=各组的区间中点值×该区间的频率之和计算即可．

解答 解：（I）由题意得，当X∈[100，130）时，
T=500X-300（130-X）=800X-39000，
当X∈[130，150]时，T=500×130=65000，
∴T=$\left\{\begin{array}{l}{800X-3900，X∈[100，130）}\\{65000，X∈[130，150]}\end{array}\right.$．
（II）由（I）知，利润T不少于57000元，
当且仅当120≤X≤150．
由直方图知需求量X∈[120，150]的频率为0.7，
所以下一个销售季度的利润T不少于57000元的概率的估计值为0.7；
（Ⅲ）以各组的区间中点值代表该组的各个值，依题意可得T的分布列如图，

T	45000	53000	61000	65000
p	0.1	0.2	0.3	0.4

所以ET=45000×0.1+53000×0.2+61000×0.3+65000×0.4=59400．
估计T的平均值为59400元．

点评 本题考查用样本的频率分布估计总体分布及识图的能力，求解的重点是对题设条件及直方图的理解，了解直方图中每个小矩形的面积的意义，是中档题．