题目内容
10．已知复数$z=\frac{1}{1+i}$，则$\overline z•i$在复平面内对应的点位于第二象限．分析 利用复数代数形式的乘除运算化简z，求出$\overline{z}$，进一步得到$\overline z•i$在复平面内对应的点的坐标得答案．
解答 解：∵$z=\frac{1}{1+i}$=$\frac{1-i}{（1+i）（1-i）}=\frac{1}{2}-\frac{i}{2}$，
∴$\overline z•i$=$（\frac{1}{2}+\frac{i}{2}）•i=-\frac{1}{2}+\frac{i}{2}$，
则$\overline z•i$在复平面内对应的点的坐标为（$-\frac{1}{2}，\frac{1}{2}$），位于第二象限．
故答案为：二．
点评 本题考查复数代数形式的乘除运算，考查复数的代数表示法及其几何意义，是基础题．
练习册系列答案
相关题目
20．已知函数f（x）=x2+bx+c且f（-1）=f（3），则（ ）
| A． | f （1）＞c＞f （-1） | B． | f （1）＜c＜f （-1） | C． | c＞f （-1）＞f （1） | D． | c＜f （-1）＜f （1） |
1．已知任意角α的终边经过点P（-3，m），且cosα=-$\frac{3}{5}$，则sinα=（ ）
| A． | -$\frac{4}{5}$ | B． | $\frac{4}{5}$ | C． | ±$\frac{4}{5}$ | D． | ±$\frac{3}{5}$ |
15．设f（x）是定义在R上的函数，其导函数为f′（x），若f（x）+f′（x）＜1，f（0）=11，则不等式f（x）＞$\frac{{e}^{x}+10}{{e}^{x}}$（其中e为自然对数的底数）的解集为（ ）
| A． | （10，+∞） | B． | （-∞，0）∪（11，+∞） | C． | （-∞，11） | D． | （-∞，0） |
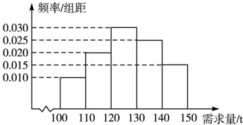经销商经销某种农产品，在一个销售季度内，每售出1t该产品获利润500元，未售出的产品，每1t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130t该农产品．以X（单位：t，100≤X≤150）表示下一个销售季度内的市场需求量，T（单位：元）表示下一个销售季度内经销该农产品的利润．