题目内容
1.已知函数f(x)=x(x-a)(x-b).(1)若a=0,b=3,求y=f(x)的切线中与y轴垂直的切线方程.
(2)若a=0,b=3,函数f(x)在(t,t+3)上既能取到极大值,又能取到极小值,求t的取值范围;
(3)当a=0时,$\frac{f(x)}{x}$+lnx+1≥0对任意的x∈[$\frac{1}{2}$,+∞)恒成立,求b的取值范围.
分析 (1)若a=0,b=3,求导数,令f′(x)=得x=0或2,即可求y=f(x)的切线中与y轴垂直的切线方程.
(2)得出函数f(x)在x=0处取得极大值,在x=2处取得极小值.函数f(x)在(t,t+3)上既能取到极大值,又能取到极小值,则只要t<0且t+3>2即可;
(3)问题转化为b≤x+$\frac{lnx}{x}$+$\frac{1}{x}$在对任意的x∈[$\frac{1}{2}$,+∞)恒成立.令g(x)=x+$\frac{lnx}{x}$+$\frac{1}{x}$,则g′(x)=$\frac{{x}^{2}-lnx}{{x}^{2}}$.求出函数的最小值,即可得出结论.
解答 解:(1)当a=0,b=3时,f(x)=x3-3x2,f′(x)=3x2-6x,
令f′(x)=得x=0或2,∴y=0或-4;
(2)当a=0,b=3时,f(x)=x3-3x2,f′(x)=3x2-6x,
令令f′(x)=得x=0或2,根据导数的符号可以得出函数f(x)在x=0处取得极大值,在x=2处取得极小值.
函数f(x)在(t,t+3)上既能取到极大值,又能取到极小值,则只要t<0且t+3>2即可,
即只要-1<t<0即可.
所以t的取值范围是(-1,0).
(3)当a=0时,$\frac{f(x)}{x}$+lnx+1≥0对任意的x∈[$\frac{1}{2}$,+∞)恒成立,
即x2-bx+lnx+1≥0对任意的x∈[$\frac{1}{2}$,+∞)恒成立,
也即b≤x+$\frac{lnx}{x}$+$\frac{1}{x}$在对任意的x∈[$\frac{1}{2}$,+∞)恒成立.
令g(x)=x+$\frac{lnx}{x}$+$\frac{1}{x}$,则g′(x)=$\frac{{x}^{2}-lnx}{{x}^{2}}$.
记m(x)=x2-lnx,则m′(x)=$\frac{2{x}^{2}-1}{x}$,
则这个函数在其定义域内有唯一的极小值点x=$\frac{\sqrt{2}}{2}$,故也是最小值点,
所以m(x)≥$\frac{1}{2}-ln\frac{\sqrt{2}}{2}$>0,从而g′(x)>0,
所以函数g(x)在[$\frac{1}{2}$,+∞)单调递增.函数g(x)min=$\frac{5}{2}$-2ln2.
故只要b≤$\frac{5}{2}$-2ln2即可.所以b的取值范围是(-∞,$\frac{5}{2}$-2ln2]. (8分)
点评 本题考查导数知识的综合运用,考查导数的几何意义、极值,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案| A. | -5<x<0或x>5 | B. | x<-5或x>5 | C. | -5<x<5 | D. | x<-5或0<x<5 |
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
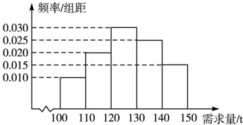 经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.