题目内容
2.数列{an}满足:a1=$\frac{4}{3}$,且an+1=$\frac{4(n+1){a}_{n}}{3{a}_{n}+n}$,(n∈N+),则$\frac{1}{{a}_{1}}$+$\frac{2}{{a}_{2}}$+$\frac{3}{{a}_{3}}$+…+$\frac{2016}{{a}_{2016}}$=$2015\frac{2}{3}+\frac{1}{3•{4}^{2016}}$.分析 由已知数列递推式可得$\frac{n+1}{{a}_{n+1}}-1=\frac{1}{4}(\frac{n}{{a}_{n}}-1)$,即数列{$\frac{n}{{a}_{n}}-1$}是以-$\frac{1}{4}$为首项,以$\frac{1}{4}$为公比的等比数列,求出等比数列的通项公式,作和即可求得$\frac{1}{{a}_{1}}$+$\frac{2}{{a}_{2}}$+$\frac{3}{{a}_{3}}$+…+$\frac{2016}{{a}_{2016}}$.
解答 解:由an+1=$\frac{4(n+1){a}_{n}}{3{a}_{n}+n}$,得$\frac{{a}_{n+1}}{n+1}=\frac{4{a}_{n}}{3{a}_{n}+n}$,
∴$\frac{n+1}{{a}_{n+1}}=\frac{1}{4}•\frac{n}{{a}_{n}}+\frac{3}{4}$,则$\frac{n+1}{{a}_{n+1}}-1=\frac{1}{4}(\frac{n}{{a}_{n}}-1)$,
又$\frac{1}{{a}_{1}}-1=\frac{3}{4}-1=-\frac{1}{4}$.
∴数列{$\frac{n}{{a}_{n}}-1$}是以-$\frac{1}{4}$为首项,以$\frac{1}{4}$为公比的等比数列,
则$\frac{n}{{a}_{n}}-1=-\frac{1}{4}•(\frac{1}{4})^{n-1}$,$\frac{n}{{a}_{n}}=1-\frac{1}{{4}^{n}}$.
∴$\frac{1}{{a}_{1}}$+$\frac{2}{{a}_{2}}$+$\frac{3}{{a}_{3}}$+…+$\frac{2016}{{a}_{2016}}$=$1-\frac{1}{4}+1-\frac{1}{{4}^{2}}+…+1-\frac{1}{{4}^{2016}}$
=2016-($\frac{1}{4}+\frac{1}{{4}^{2}}+…+\frac{1}{{4}^{2016}}$)=$2016-\frac{\frac{1}{4}(1-\frac{1}{{4}^{2016}})}{1-\frac{1}{4}}$=$2015\frac{2}{3}+\frac{1}{3•{4}^{2016}}$.
故答案为:$2015\frac{2}{3}+\frac{1}{3•{4}^{2016}}$.
点评 本题考查数列递推式,考查了等比关系的确定,考查等比数列前n项和的求法,是中档题.

| A. | y轴对称 | B. | 直线y=x对称 | C. | 坐标原点对称 | D. | 直线y=-x对称 |

| A. | A∩∁UB | B. | B∩∁UA | C. | ∁U(A∩B) | D. | ∁U(A∪B) |
| A. | 3x+2y=0 | B. | 3x-2y=0 | C. | 2x+3y=0 | D. | 2x-3y=0 |
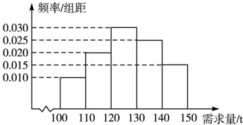 经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.