题目内容
7.已知命题p:?x0∈R,x0-2>0,命题q:?x∈R,$\sqrt{x}$<x,则下列说法中正确的是( )| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
分析 先判断命题p,q的真假,进而根据复合命题真假判断的真值表,得到答案.
解答 解:?x0=3∈R,x0-2>0,故命题p为真命题;
当x∈[0,1]时,$\sqrt{x}$≥x,故命题q为假命题,
故命题p∨q是真命题,
命题p∧q是假命题,
命题p∧(¬q)是真命题,
命题p∨(¬q)是真命题,
故选:C.
点评 本题以命题的真假判断与应用为载体,考查了复合命题,全称命题,特称命题等知识点,难度中档.

练习册系列答案
相关题目
15.设f(x)=$\left\{\begin{array}{l}{{k}^{2}x+{a}^{2}-k(x≥0)}\\{{x}^{2}+({a}^{2}+4a)x+(2-a)^{2}(x<0)}\end{array}\right.$,其中a∈R,若对任意的非零实数x1,存在唯一的非零实数x2(x1≠x2),使得f(x2)=f(x1)成立,则k的取值范围为( )
| A. | [-20,-4] | B. | [-30,-9] | C. | [-4,0] | D. | [-9,-4] |
19.已知向量,$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(3,-2),且($\overrightarrow{a}$+$\overrightarrow{b}$)∥$\overrightarrow{b}$,则m=( )
| A. | $-\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -8 | D. | 8 |
16.若R上的可导函数f(x)满足f(x)=x2-xf'(1)+1,则f'(0)=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
17.函数f(x)=x-$\frac{1}{x}$的图象关于( )
| A. | y轴对称 | B. | 直线y=x对称 | C. | 坐标原点对称 | D. | 直线y=-x对称 |
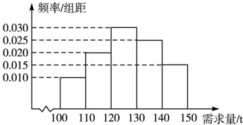 经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.