题目内容
20.在锐角△ABC中,角A,B,C所对的边分别为a,b,c,已知a=bcosC+$\frac{\sqrt{3}}{3}$csinB.(1)若a=2,b=$\sqrt{7}$,求c
(2)设函数y=$\sqrt{3}$sin(2A-30°)-2sin2(C-15°),求y的取值范围.
分析 (1)由已知利用正弦定理,三角函数恒等变换的应用化简可得tanB=$\sqrt{3}$,可求∠B=$\frac{π}{3}$,利用余弦定理即可解得c的值.
(2)利用三角函数恒等变换的应用化简可得y=$\sqrt{3}$sin(2A-60°)-1,结合范围A∈($\frac{π}{6}$,$\frac{π}{2}$),利用正弦函数的性质即可得解取值范围.
解答 (本题满分为12分)
解:(1)∵a=bccosC+$\frac{\sqrt{3}}{3}$csinB,
∴sinA=sinBcosC+$\frac{\sqrt{3}}{3}$sinCsinB,
∴cosBsinC=$\frac{\sqrt{3}}{3}$sinCsinB,
∴tanB=$\sqrt{3}$,
∴∠B=$\frac{π}{3}$.…(4分)
∵b2=a2+c2-2accosB,
∴c2-2c-3=0,
∴c=3.…(6分)
(2)∵y=$\sqrt{3}$sin(2A-30°)-2sin2(C-15°)
=$\sqrt{3}$sin(2A-30°)-1+2cos(2C-30°)
=$\sqrt{3}$sin(2A-30°)-cos(2A-30°)-1
=$\sqrt{3}$sin(2A-60°)-1,…(10分)
又∵△ABC为锐角三角形,
∴A∈($\frac{π}{6}$,$\frac{π}{2}$),
∴y∈(-1,1].…(12分)
点评 本题主要考查了正弦定理,三角函数恒等变换的应用,余弦定理,正弦函数的图象和性质在解三角形中的应用,考查了转化思想,属于中档题.

练习册系列答案
相关题目
11.函数$y={(\frac{1}{3})^{|x|}}-1$的值域是( )
| A. | [1,+∞) | B. | [0,+∞) | C. | (-∞,0] | D. | (-1,0] |
15.已知函数f(x)=sin2x+sinx+cosx,以下说法中不正确的是( )
| A. | f(x)周期为2π | B. | f(x)最小值为-$\frac{5}{4}$ | ||
| C. | f(x)在区间[0,$\frac{π}{2}$]单调递增 | D. | f(x)关于点x=$\frac{π}{4}$对称 |
5.已知集合$A=\left\{{\left.x\right|\frac{x}{x-1}≥0,x∈R}\right\},B=\left\{{\left.y\right|y=3{x^2}+1,x∈R}\right\}$,则A∩B=( )
| A. | (1,+∞) | B. | [1,+∞) | C. | (-∞,0]∪(1,+∞) | D. | [0,1] |
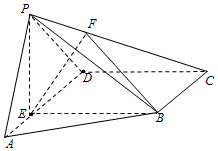 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.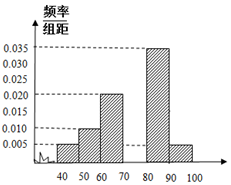 为了估计某校的一次数学考试情况,现从该校参加考试的600名学生中随机抽出60名学生,其成绩(百分制)均在[40,100)上,将这些成绩分成六段[40,50),[50,60)…[90,100),后得到如图所示部分频率分布直方图.
为了估计某校的一次数学考试情况,现从该校参加考试的600名学生中随机抽出60名学生,其成绩(百分制)均在[40,100)上,将这些成绩分成六段[40,50),[50,60)…[90,100),后得到如图所示部分频率分布直方图.