题目内容
16.已知$f({log_3}x)={x^2}-2x+4$,$x∈[\frac{1}{3},3]$.(1)求f(x)的解析式及定义域;
(2)求f(x)的值域;
(2)若方程f(x)=a2-3a+3有实数根,求实数a的取值范围.
分析 (1)设t=log3x,得到t∈[-1,1],从而求出f(x)的解析式和函数的定义域即可;
(2)设u=3x,得到$u∈[\frac{1}{3},3]$,求出f(u),从而求出函数的值域即可;
(3)求出a2-3a+3∈[3,7],从而求出a的范围即可.
解答 解:(1)设t=log3x,t∈[-1,1],则x=3t-------(3分)
f(t)=(3t)2-2•3t+4,
∴f(x)=(3x)2-2•3x+4,
f(x)的定义域为[-1,1]---(6分)
(2)设u=3x,$u∈[\frac{1}{3},3]$,
f(u)=u2-2u+4=(u-1)2+3,
∴f(u)∈[3,7]
即所求值域为[3,7]----------(9分)
(3)由于方程f(x)=a2-3a+3有实数根,
∴a2-3a+3∈[3,7],
∴a∈[-1,0]∪[3,4]-----------(12分)
点评 本题考查了对数函数以及指数函数的性质,考查函数的定义域、值域问题,是一道中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
6.下列四组中的f(x),g(x),表示同一个函数的是( )
| A. | f(x)=1,g(x)=x0 | B. | f(x)=x-1,g(x)=$\frac{x^2}{x}$-1 | ||
| C. | f (x)=x2,g(x)=($\sqrt{x}$)4 | D. | f(x)=|x|,g(x)=$\sqrt{x^2}$ |
4.已知y=f(x)是定义在R上的增函数且为奇函数,若对任意的x,y∈R,不等式f(x2-6x+21)+f(y2-8y)<0恒成立,则当x>3时,x2+y2的取值范围是( )
| A. | (3,7) | B. | (9,25) | C. | (13,49) | D. | (9,49) |
11.函数$y={(\frac{1}{3})^{|x|}}-1$的值域是( )
| A. | [1,+∞) | B. | [0,+∞) | C. | (-∞,0] | D. | (-1,0] |
5.已知集合$A=\left\{{\left.x\right|\frac{x}{x-1}≥0,x∈R}\right\},B=\left\{{\left.y\right|y=3{x^2}+1,x∈R}\right\}$,则A∩B=( )
| A. | (1,+∞) | B. | [1,+∞) | C. | (-∞,0]∪(1,+∞) | D. | [0,1] |
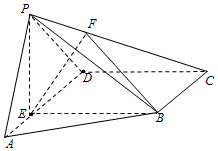 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.