题目内容

12．已知双曲线${x^2}-\frac{y^2}{b^2}=1（b＞0）$的一条渐近线过点（1，2），则b=2，其离心率为$\sqrt{5}$．

分析 利用双曲线的渐近线经过的点，直接求出b，然后求解离心率即可．

解答 解：双曲线${x^2}-\frac{y^2}{b^2}=1（b＞0）$的一条渐近线y=bx，过点（1，2），可得b=2，
a=1，c=$\sqrt{5}$，
可得双曲线的离心率为：e=$\sqrt{5}$．
故答案为：2；$\sqrt{5}$．

点评 本题考查双曲线的简单性质的应用，考查计算能力．

练习册系列答案
相关题目
18．△ABC中，E是边AC的中点，$\overrightarrow{BC}$=4$\overrightarrow{BD}$．
（1）若$\overrightarrow{DE}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$，求x，y的值；
（2）已知AB=2，AC=4，∠BAC=60°，求$\overrightarrow{DE}$•$\overrightarrow{BC}$的值．
19．（1）化简：log89×log32-lg5-lg2+lne2
（2）化简：（-2${a}^{\frac{1}{3}}$${b}^{-\frac{3}{4}}$）•（-${a}^{\frac{1}{2}}$${b}^{-\frac{1}{3}}$）÷（-3${a}^{\frac{2}{3}}{b}^{-\frac{1}{4}}$）
16．两圆x2+y2=16与（x-4）2+（y+3）2=r2（r＞0）在交点处的切线互相垂直，则r=（　　）
A．5B．4C．3D．2$\sqrt{2}$
7．若$a=\int_1^2{2^x}dx$，$b=\int_1^2xdx$，$c=\int_1^2{{{log}_2}x}dx$，则a，b，c的大小关系是（　　）
A．c＜b＜aB．b＜c＜aC．c＜a＜bD．a＜b＜c
17．已知f（x）是奇函数，若x＞0时，f（x）=sinx+cosx，则x＜0时，f（x）=sinx-cosx．
4．下列命题中真命题是（2）（4）．
（1）若|$\overrightarrow{a}$|=1，则$\overrightarrow{a}$=±1；
（2）若$\overrightarrow{a}$≠$\overrightarrow{0}$，则$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$是单位向量；
（3）若$\overrightarrow{a}$∥$\overrightarrow{b}$，$\overrightarrow{b}$∥$\overrightarrow{c}$，则$\overrightarrow{a}$∥$\overrightarrow{c}$；
（4）若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|，则$\overrightarrow{a}$、$\overrightarrow{b}$共线．
1．过抛物线y2=4x的焦点F的直线l交该抛物线于A，B两点，点A在第一象限，若|AF|=3，则直线l的斜率为（　　）
A．1B．$\sqrt{2}$C．$\sqrt{3}$D．$2\sqrt{2}$
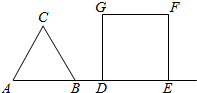2．如图所示，A、B、D、E四点在同一直线上，△ABC是边长为2的正三角形，DEFG是边长为2的正方形，在静止状态时，B点在D点的左侧，且$|{\overrightarrow{BD}}|=1$，让A点沿直线AB从左到右运动，当A点运动到E点时，运动结束．
（1）求在静止状态时，$\overrightarrow{BF}•\overrightarrow{CE}$的值；
（2）当A点运动时，求$\overrightarrow{BF}•\overrightarrow{CE}$的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网