题目内容
 如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(2,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=
如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(2,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=| 1 |
| 2 |
考点:待定系数法求直线方程
专题:直线与圆
分析:由题意分别求出直线OA、OB的方程,由方程设出A、B的坐标,由中点坐标公式求出点C的坐标,利用C在直线y=
x上和三点共线:斜率相等,列出方程组求出方程的解,即可求出A的坐标,结合P(2,0)求出直线AB的斜率,代入点斜式方程再化简即可得直线AB的方程.
| 1 |
| 2 |
解答:
 解:由题意可得kOA=1,kOB=-
解:由题意可得kOA=1,kOB=-
,
所以直线OA的方程为y=x,直线OB的方程为y=-
x.
设A(m,m),B(-
n,n),
所以AB的中点C的坐标为(
,
),
因为点C在y=
x直线上,且A、P、B三点共线,
所以
,解得m=2
,…(8分)
所以A(2
,2
).
又P(2,0),所以kAB=kAP=
=
,
所以直线AB的方程为:y=
(x-2),即(3+
)x-2y-6-2
=0.…(12分)
 解:由题意可得kOA=1,kOB=-
解:由题意可得kOA=1,kOB=-
| ||
| 3 |
所以直线OA的方程为y=x,直线OB的方程为y=-
| ||
| 3 |
设A(m,m),B(-
| 3 |
所以AB的中点C的坐标为(
m-
| ||
| 2 |
| m+n |
| 2 |
因为点C在y=
| 1 |
| 2 |
所以
|
| 3 |
所以A(2
| 3 |
| 3 |
又P(2,0),所以kAB=kAP=
2
| ||
2
|
3+
| ||
| 2 |
所以直线AB的方程为:y=
3+
| ||
| 2 |
| 3 |
| 3 |
点评:本题考查直线的有关知识:中点坐标公式、点斜式方程、三点共线:斜率相等,以及方程思想,考查计算能力.

练习册系列答案
相关题目
等差数列{an}的前n项和为Sn,如果a1=2,a3+a5=22,那么S3等于( )
| A、8 | B、15 | C、24 | D、30 |
设等差数列{an}的前n项和为Sn,若a3+a9=4,则S11等于( )
| A、12 | B、18 | C、22 | D、44 |
已知集合A={0,1},B={x|x⊆A},则A与B的关系为( )
| A、A⊆B | B、B⊆A |
| C、A∈B | D、A∉B |
已知a=2log32,b=log
2,c=2-
,则a,b,c的大小关系是( )
| 1 |
| 4 |
| 1 |
| 3 |
| A、a>b>c |
| B、c>b>a |
| C、c>a>b |
| D、a>c>b |
若角α的终边经过点P(-3,4),则tanα=( )
A、
| ||
B、-
| ||
C、-
| ||
D、-
|
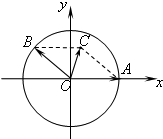 如图所示,在xOy平面上,点A(1,0),点B在单位圆上.∠AOB=θ(0<θ<π)
如图所示,在xOy平面上,点A(1,0),点B在单位圆上.∠AOB=θ(0<θ<π)