题目内容
5.要得到余弦曲线y=cosx,只需将正弦曲线y=sinx向左平移( )| A. | $\frac{π}{2}$个单位 | B. | $\frac{π}{3}$个单位 | C. | $\frac{π}{4}$个单位 | D. | $\frac{π}{6}$个单位 |
分析 根据诱导公式,知cosx=sin(x-$\frac{π}{2}$),所以y=cosx=sin(x-$\frac{π}{2}$),根据平移变换的规律,当x减去某数时,图象向左平移,可以知要得到余弦曲线,只需将正弦曲线向左平移$\frac{π}{2}$个单位.
解答 解:∵cosx=sin(x-$\frac{π}{2}$)
∴余弦函数y=cosx的图象可看作正弦y=sinx图象向左平移$\frac{π}{2}$个单位得到.
故选:A
点评 本题主要考察了利用诱导公式和平移变换规律来判断三角函数图象,做题时记清平移方向,属于基础题.

练习册系列答案
相关题目
15.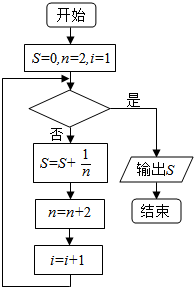 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )
 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )| A. | i>48 | B. | i>24 | C. | i<48 | D. | i<24 |
16.如图所示,程序框图(算法流程图)的输出结果是( )


| A. | -2 | B. | 0 | C. | =-1 | D. | -3 |
13.函数f(x)=log0.8(2x2-ax+3)在(-1,+∞)为减函数,则a的范围( )
| A. | (-5,-4] | B. | [-5,-4] | C. | (-∞,-4) | D. | (-∞,-4] |
10.在空间直角坐标系Oxyz中,若y轴上点M到两点P(1,0,2),Q(1,-3,1)的距离相等,则点M的坐标为( )
| A. | (0,1,0) | B. | (0,-1,0) | C. | (0,0,3) | D. | (0,0,-3) |
14.已知a,b为实数,则“a+b≤2”是“a≤1且b≤1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 已知x=$\frac{π}{6}$是函数f(x)=sin(2x+φ)(0<φ<$\frac{π}{2}$)图象的一条
已知x=$\frac{π}{6}$是函数f(x)=sin(2x+φ)(0<φ<$\frac{π}{2}$)图象的一条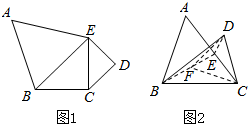 如图1,平面五边形ABCDE中,△ABE是边长为2的正三角形,△BCE、△CDE均为等腰直角三角形,且∠BCE和∠CDE为直角,现将△ABE、△CDE分别沿BE、CE折起,使平面ABE⊥平面BCE,平面DCE⊥平面BCE,如图2所示.
如图1,平面五边形ABCDE中,△ABE是边长为2的正三角形,△BCE、△CDE均为等腰直角三角形,且∠BCE和∠CDE为直角,现将△ABE、△CDE分别沿BE、CE折起,使平面ABE⊥平面BCE,平面DCE⊥平面BCE,如图2所示.