题目内容
4.已知三棱锥P-ABC,PA⊥面ABC,AB⊥BC,且PA=AB=BC=2,则三棱锥P-ABC的外接球的表面积为12π.分析 确定PC的中点O为球心,求出球的半径,利用球的表面积公式,即可求得结论.
解答  解:∵PA⊥面ABC,BC?面ABC,
解:∵PA⊥面ABC,BC?面ABC,
∴PA⊥BC
∵AB⊥BC,PA∩AB=A
∴BC⊥面PAB
∵PB?面PAB
∴BC⊥PB
取PC的中点O,则OP=OA=OB=OC,∴O为球心
∵PA=2,∴PC=2$\sqrt{3}$
∴球半径为r=$\sqrt{3}$
∴该三棱锥的外接球的表面积为4πr2=12π
故答案为:12π.
点评 本题考查球的表面积,解题的关键是确定球心与半径,属于基础题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
15.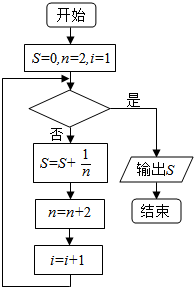 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )
 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )| A. | i>48 | B. | i>24 | C. | i<48 | D. | i<24 |
16.如图所示,程序框图(算法流程图)的输出结果是( )


| A. | -2 | B. | 0 | C. | =-1 | D. | -3 |
13.函数f(x)=log0.8(2x2-ax+3)在(-1,+∞)为减函数,则a的范围( )
| A. | (-5,-4] | B. | [-5,-4] | C. | (-∞,-4) | D. | (-∞,-4] |
14.已知a,b为实数,则“a+b≤2”是“a≤1且b≤1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |