题目内容
3.函数y=tan(2x+$\frac{π}{4}$)的单调递增区间是($\frac{kπ}{2}$-$\frac{3π}{8}$,$\frac{kπ}{2}$+$\frac{π}{8}$),k∈Z.分析 根据正切函数y=tanx的单调增区间,令kπ-$\frac{π}{2}$<2x+$\frac{π}{4}$<kπ+$\frac{π}{2}$,k∈Z;
求出不等式组的解集即可.
解答 解:函数y=tan(2x+$\frac{π}{4}$),
令kπ-$\frac{π}{2}$<2x+$\frac{π}{4}$<kπ+$\frac{π}{2}$,k∈Z;
解得kπ-$\frac{3π}{4}$<2x<kπ+$\frac{π}{4}$,k∈Z,
即$\frac{kπ}{2}$-$\frac{3π}{8}$<x<$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z;
所以函数y=2tan(2x+$\frac{π}{4}$)的单调递增区间是:
($\frac{kπ}{2}$-$\frac{3π}{8}$,$\frac{kπ}{2}$+$\frac{π}{8}$),k∈Z.
故答案为:($\frac{kπ}{2}$-$\frac{3π}{8}$,$\frac{kπ}{2}$+$\frac{π}{8}$),k∈Z.
点评 本题考查了正切函数的单调性以及整体代换的应用问题,是基础题.

练习册系列答案
相关题目
12.过抛物线y2=4x的焦点F作互相垂直的弦AC,BD,则点A,B,C,D所构成四边形的面积的最小值为( )
| A. | 16 | B. | 32 | C. | 48 | D. | 64 |
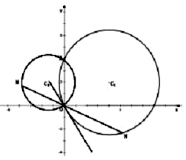 已知圆${C_1}:{({x-4})^2}+{({y-2})^2}=20$与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;
已知圆${C_1}:{({x-4})^2}+{({y-2})^2}=20$与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;