题目内容
15.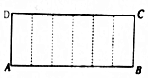 已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )
已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )| A. | 13π | B. | 12π | C. | 11π | D. | 10π |
分析 正六棱柱的底面边长为x,高为y,则6x+y=9,0<x<1.5,表示正六棱柱的体积,利用基本不等式求最值,求出正六棱柱的外接球的半径,即可求出外接球的表面积.
解答 解:设正六棱柱的底面边长为x,高为y,则6x+y=9,0<x<1.5,
正六棱柱的体积V=$6×\frac{\sqrt{3}}{4}{x}^{2}y$=$\frac{\sqrt{3}}{6}$•3x•3x•(9-6x)≤$\frac{\sqrt{3}}{6}[\frac{3x+3x+(9-6x)}{3}]^{3}$=$\frac{9\sqrt{3}}{2}$,
当且仅当x=1时,等号成立,此时y=3,
可知正六棱柱的外接球的球心是其上下底面中心连线的中点,则半径为$\sqrt{1+\frac{9}{4}}$=$\frac{\sqrt{13}}{2}$,
∴外接球的表面积为4$π×\frac{13}{4}$=13π.
故选A.
点评 本题考查外接球的表面积,考查基本不等式的运用,确定正六棱柱的外接球的半径是关键.

练习册系列答案
相关题目
6.若复数$z=\frac{1-i}{i}$(i为虚数单位),则z的共轭复数$\overline z$=( )
| A. | 1+i | B. | -1+i | C. | l-i | D. | -1一i |
10.关于平面向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$,下列判断中正确的是( )
| A. | 若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,则$\overrightarrow{b}$=$\overrightarrow{c}$ | B. | 若$\overrightarrow{a}$=(1,k),$\overrightarrow{b}$=(-2,6),$\overrightarrow{a}$∥$\overrightarrow{b}$,则k=$\frac{1}{3}$ | ||
| C. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$•$\overrightarrow{b}$=0 | D. | 若$\overrightarrow{a}$与$\overrightarrow{b}$是单位向量,则$\overrightarrow{a}$•$\overrightarrow{b}$=1 |
7.方程x2+2x+n2=0(n∈[-1,2])有实根的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
5.在△OMN中,点A在OM上,点B在ON上,且AB∥MN,2OA=OM,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则终点P落在四边形ABNM内(含边界)时,$\frac{y+x+2}{x+1}$的取值范围是( )
| A. | $[\frac{1}{2},2]$ | B. | $[\frac{1}{3},3]$ | C. | $[\frac{3}{2},3]$ | D. | $[\frac{4}{3},4]$ |
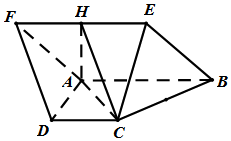 如图所示,菱形ABEF⊥直角梯形ABCD,∠BAD=∠CDA=90°,∠ABE=60°,AB=2AD=2CD=2,H是EF的中点
如图所示,菱形ABEF⊥直角梯形ABCD,∠BAD=∠CDA=90°,∠ABE=60°,AB=2AD=2CD=2,H是EF的中点