题目内容
17.函数$y={log_a}({2{x^2}-3x+1})$,当x=3时,y<0则该函数的单调递减区间是( )| A. | $({-∞,\frac{3}{4}})$ | B. | $({\frac{3}{4},+∞})$ | C. | $({-∞,\frac{1}{2}})$ | D. | (1,+∞) |
分析 根据x=3,y<0,求解a的范围,再根据复合函数的单调性“同增异减”判断即可.
解答 解:函数$y={log_a}({2{x^2}-3x+1})$,当x=3时,y<0,
当x=3时,2x2-3x+1=10,即loga10<0,
可得:0<a<1,
令函数2x2-3x+1=u,(u>0)则y=logau是减函数,
函数u=2x2-3x+1,开口向上,对称轴为x=$\frac{3}{4}$,
∵u>0,
即2x2-3x+1>0,
解得:x>1或x<$\frac{1}{2}$.
∴函数u在(1,+∞)单调递增,
函数u在(-∞,$\frac{1}{2}$)单调递减,
根据复合函数的单调性“同增异减”可得该函数单调递减区间为(1,+∞).
故选D
点评 本题考查了不等式的计算和单调性的运用,以及复合函数的单调性“同增异减”的判断,属于基础题.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
7.方程x2+2x+n2=0(n∈[-1,2])有实根的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
8.两圆x2+y2-4x+2y+1=0与x2+y2+4x-4y-1=0的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
5.在△OMN中,点A在OM上,点B在ON上,且AB∥MN,2OA=OM,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则终点P落在四边形ABNM内(含边界)时,$\frac{y+x+2}{x+1}$的取值范围是( )
| A. | $[\frac{1}{2},2]$ | B. | $[\frac{1}{3},3]$ | C. | $[\frac{3}{2},3]$ | D. | $[\frac{4}{3},4]$ |
7.tan$\frac{π}{4}$等于( )
| A. | -1 | B. | 1 | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
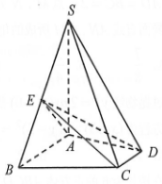 如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD=2,E是边SB的中点.
如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD=2,E是边SB的中点.