题目内容
要使函数y=ax+b有零点，则实数b的取值范围是 ．
考点：函数零点的判定定理
专题：计算题,函数的性质及应用
分析：函数y=ax+b有零点可化为方程ax+b=0有解，由ax＞0可确定b的取值范围．
解答：
解：函数y=ax+b有零点可化为方程ax+b=0有解，
即b=-ax有解，
∵ax＞0，
∴b＜0；
故实数b的取值范围是（-∞，0）；
故答案为：（-∞，0）．
即b=-ax有解，
∵ax＞0，
∴b＜0；
故实数b的取值范围是（-∞，0）；
故答案为：（-∞，0）．
点评：本题考查了函数的零点与方程的关系应用，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，AC1是正方体的一条体对角线，点P，Q分别为其在棱的中点，则PQ与AC1所成的角为（ ）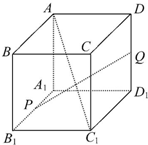 
A、
| ||
B、
| ||
C、
| ||
D、
|
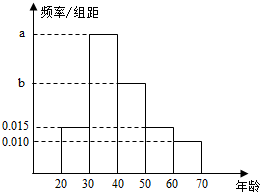根据某电子商务平台的调查统计显示，参与调查的1000位上网购物者的年龄情况如图显示．设变量x，y满足|x-1|+|y-a|≤1，若2x+y的最大值是5，则实数a的值是（ ）
| A、2 | B、1 | C、0 | D、-1 |