题目内容
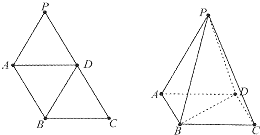 如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形,将它沿AD折成大小为α(
如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形,将它沿AD折成大小为α(| π |
| 2 |
(Ⅰ)证明:AD⊥PB;
(Ⅱ)当α=120°时,求PC与平面ABCD所成角的正切值.
考点:直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(Ⅰ)首先通过做中点,利用三角形PAD为等边三角形,及菱形ABCD中,AB=BD=2,得到PE⊥AD,BE⊥AD,得到AD⊥平面PBE,进一步求得结论.
(Ⅱ)利用二面角的平面角,进一步作出PF⊥平面ABCD,进一步利用余弦定理解得:BE=
,PF=
,EF=
同理在△CDE中,ED=1,CD=2,∠EDC=120°,利用余弦定理解得:EC=
,利用余弦定理,
解得:cos∠BEC=
=
,所以在△CEF中,利用余弦定理:
CF2=EF2+EC2-2EF•ECcos∠FEC,解得:CF=
,最后求出结论.
(Ⅱ)利用二面角的平面角,进一步作出PF⊥平面ABCD,进一步利用余弦定理解得:BE=
| 3 |
| 3 |
| 2 |
| ||
| 2 |
同理在△CDE中,ED=1,CD=2,∠EDC=120°,利用余弦定理解得:EC=
| 7 |
解得:cos∠BEC=
| 3+7-4 | ||||
2
|
| ||
| 7 |
CF2=EF2+EC2-2EF•ECcos∠FEC,解得:CF=
| ||
| 2 |
解答:
证明:(Ⅰ)在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形,
取AD的中点E,连接PE,BE,
所以:PE⊥AD,BE⊥AD,
则:AD⊥平面PBE,
所以:AD⊥PB.
(Ⅱ)将它沿AD折成大小为120°的二面角P-AD-B,
所以∠PEF=60°,过P做PF⊥平面ABCD,交BE的延长线于F,
连接CF,所以:∠PCF即是PC与平面ABCD所成的角.
在△ABE中,AB=2,AE=1,∠ABE=60°
利用余弦定理解得:BE=
在△PEF中,
解得:PF=
,EF=
同理在△CDE中,ED=1,CD=2,∠EDC=120°
利用余弦定理解得:EC=
则:在△BEC中,利用余弦定理,
解得:cos∠BEC=
=
所以在△CEF中,利用余弦定理:
CF2=EF2+EC2-2EF•ECcos∠FEC
解得:CF=
在直角三角形PCF中,tan∠PCF=
=
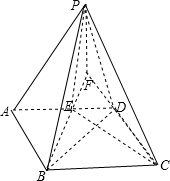
取AD的中点E,连接PE,BE,
所以:PE⊥AD,BE⊥AD,
则:AD⊥平面PBE,
所以:AD⊥PB.
(Ⅱ)将它沿AD折成大小为120°的二面角P-AD-B,
所以∠PEF=60°,过P做PF⊥平面ABCD,交BE的延长线于F,
连接CF,所以:∠PCF即是PC与平面ABCD所成的角.
在△ABE中,AB=2,AE=1,∠ABE=60°
利用余弦定理解得:BE=
| 3 |
在△PEF中,
解得:PF=
| 3 |
| 2 |
| ||
| 2 |
同理在△CDE中,ED=1,CD=2,∠EDC=120°
利用余弦定理解得:EC=
| 7 |
则:在△BEC中,利用余弦定理,
解得:cos∠BEC=
| 3+7-4 | ||||
2
|
| ||
| 7 |
所以在△CEF中,利用余弦定理:
CF2=EF2+EC2-2EF•ECcos∠FEC
解得:CF=
| ||
| 2 |
在直角三角形PCF中,tan∠PCF=
| PF |
| CF |
3
| ||
| 43 |

点评:本题考查的知识要点:线面垂直的判定定理,线面垂直与线线垂直之间的转化,线面的夹角的应用,余弦定理的应用,及相关的运算问题,属于中等题型.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
实数x、y满足x2+2xy+y2+x2y2=1,则x-y的最大值为( )
| A、4 | ||
B、2
| ||
| C、2 | ||
D、
|
复数z=1+
的虚部为( )
| 1 |
| i |
| A、1 | B、i | C、-1 | D、-i |
如图所示,AC1是正方体的一条体对角线,点P,Q分别为其在棱的中点,则PQ与AC1所成的角为( ) 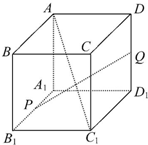

A、
| ||
B、
| ||
C、
| ||
D、
|
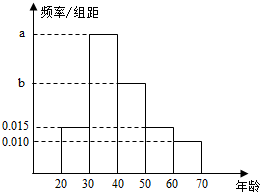 根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.
根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.