题目内容
已知椭圆C:
+
=1(a>b>0)经过点M(
,1),离心率为
.
(1)求椭圆C的方程:
(2)过点Q(1,0)的直线l与椭圆C相交于A、B两点,点P(4,3),记直线PA,PB的斜率分别为k1,k2,当k1•k2最大时,求直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
(1)求椭圆C的方程:
(2)过点Q(1,0)的直线l与椭圆C相交于A、B两点,点P(4,3),记直线PA,PB的斜率分别为k1,k2,当k1•k2最大时,求直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:
分析:(1)根据题意,椭圆C:
+
=1(a>b>0)经过点M(
,1),离心率为
,建立方程,由此算出a,b,即可得到椭圆C的方程;
(2)当直线l的斜率等于0时,结合椭圆的方程算出k1•k2;直线l的斜率不等于0时,设A(x1,y1),B(x2,y2),直线l方程为x=my+1,由直线l方程与椭圆方程消去x得到关于y的一元二次方程,利用根与系数的关系,直线的斜率公式和直线l方程化简k1•k2的式子,再根据基本不等式加以计算,可得k1•k2≤1,当且仅当m=1时,等号成立.因此当m=1时k1•k2的最大值为1,可得此时的直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
(2)当直线l的斜率等于0时,结合椭圆的方程算出k1•k2;直线l的斜率不等于0时,设A(x1,y1),B(x2,y2),直线l方程为x=my+1,由直线l方程与椭圆方程消去x得到关于y的一元二次方程,利用根与系数的关系,直线的斜率公式和直线l方程化简k1•k2的式子,再根据基本不等式加以计算,可得k1•k2≤1,当且仅当m=1时,等号成立.因此当m=1时k1•k2的最大值为1,可得此时的直线l的方程.
解答:
解:(1)∵离心率为
,
∴
=
=
,
∴a2=2b2,①
∵椭圆C:
+
=1(a>b>0)经过点M(
,1),
∴
+
=1,②
①②可得a=2,b=
.
∴椭圆C的方程为
+
=1;
(2)①直线l的斜率等于0时,A、B分别为左右顶点,
∴k1•k2=
•
=
;
②直线l的斜率不等于0时,设直线l的方程为x=my+1,A(x1,y1),B(x2,y2).
由
消去x,整理得(m2+2)y2+2my-3=0.
∴y1+y2=
,y1y2=
.
∵x1=my1+1,x2=my2+1,
∴k1•k2=
•
=
=
=
=
+
.
令t=4m+1,则
=
=
≤
,
∴k1•k2=
+
≤1,当且仅当t=5即m=1时,等号成立.
综合①②,可得k1•k2的最大值为1,此时的直线l方程为x=y+1,即x-y-1=0.
| ||
| 2 |
∴
| c2 |
| a2 |
| a2-b2 |
| a2 |
| 1 |
| 2 |
∴a2=2b2,①
∵椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
∴
| 2 |
| a2 |
| 1 |
| b2 |
①②可得a=2,b=
| 2 |
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 2 |
(2)①直线l的斜率等于0时,A、B分别为左右顶点,
∴k1•k2=
| 3 |
| 4+2 |
| 3 |
| 4-2 |
| 3 |
| 4 |
②直线l的斜率不等于0时,设直线l的方程为x=my+1,A(x1,y1),B(x2,y2).
由
|
∴y1+y2=
| -2m |
| m2+2 |
| -3 |
| m2+2 |
∵x1=my1+1,x2=my2+1,
∴k1•k2=
| 3-y1 |
| 4-x1 |
| 3-y2 |
| 4-x2 |
| (3-y1)(3-y2) |
| (3-my1)(3-my2) |
| 9-3(y1+y2)+y1y2 |
| 9-3m(y1+y2)+m2y1y2 |
| 3m2+2m+5 |
| 4m2+6 |
=
| 3 |
| 4 |
| 4m+1 |
| 8m2+12 |
令t=4m+1,则
| 4m+1 |
| 8m2+12 |
| 2t |
| t2-2t+25 |
| 2 | ||
(t+
|
| 1 |
| 4 |
∴k1•k2=
| 3 |
| 4 |
| 4m+1 |
| 8m2+12 |
综合①②,可得k1•k2的最大值为1,此时的直线l方程为x=y+1,即x-y-1=0.
点评:本题给出椭圆满足的条件,求椭圆的方程并研究直线斜率之积的最大值问题.着重考查了椭圆的标准方程与简单几何性质、直线的基本量与基本形式、用基本不等式求最值和直线与圆锥曲线的位置关系等知识,属于中档题.

练习册系列答案
相关题目
 如图,直角梯形ABCD中,∠ABC=∠BAD=90°,
如图,直角梯形ABCD中,∠ABC=∠BAD=90°,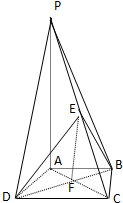 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=2,AD=4,DC=3,PA=5,E∈PC,AC∩BD=F.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=2,AD=4,DC=3,PA=5,E∈PC,AC∩BD=F.