题目内容
已知定义域为R的函数f(x)=
是奇函数.
(1)求a,b的值;
(2)用定义证明f(x)在R上为减函数;
(3)若对于任意t∈[-2,2],不等式f(t2-2t)+f(-2t2+k)<0恒成立,求k的取值范围.
| b-2x |
| 2x+a |
(1)求a,b的值;
(2)用定义证明f(x)在R上为减函数;
(3)若对于任意t∈[-2,2],不等式f(t2-2t)+f(-2t2+k)<0恒成立,求k的取值范围.
考点:奇偶性与单调性的综合,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)根据函数是R上的奇函数,利用f(0)=0,即可求出a,b的值;
(2)根据函数单调性的定义证明f(x)在R上为减函数;
(3)根据函数单调性和奇偶性的性质,将不等式f(t2-2t)+f(-2t2+k)<0恒成立进行转化,即可求k的取值范围.
(2)根据函数单调性的定义证明f(x)在R上为减函数;
(3)根据函数单调性和奇偶性的性质,将不等式f(t2-2t)+f(-2t2+k)<0恒成立进行转化,即可求k的取值范围.
解答:
解:(1)∵定义域为R的函数f(x)=
是奇函数.
∴f(0)=
=0,解得b=1.
由f(-1)=-f(1)得
=-
,
解得a=1,
此时f(x)=
,满足f(-x)=-f(x),
及函数f(x)是奇函数.
(2)用定义证明f(x)在R上为减函数;
∵f(x)=
=1+
,
设x1<x2,f(x1)-f(x2)=
-
=
,
∵x1<x2,
∴2x2-2x1>0,(1+2x1)(1+2x2)>0,
∴
>0,
∴f(x1)-f(x2)>0,
及f(x1)>f(x2),
∴函数f(x)在R上为减函数.
(3)由(1)(2)函数为奇函数且为减函数,
∴不等式f(t2-2t)+f(-2t2+k)<0恒成立,等价为
f(t2-2t)<-f(-2t2+k)=f(2t2-k),
即t2-2t>2t2-k对t∈[-2,2],
及k>t2+2t对t∈[-2,2]恒成立,
∵y=t2+2t=(t+1)2-1在t∈[-2,2]上的最大值为8,
∴k>8,
即k的取值范围是k>8.
| b-2x |
| 2x+a |
∴f(0)=
| b-1 |
| 1+a |
由f(-1)=-f(1)得
| 1-2-1 |
| 2-1+a |
| 1-2 |
| 2+a |
解得a=1,
此时f(x)=
| 1-2x |
| 1+2x |
及函数f(x)是奇函数.
(2)用定义证明f(x)在R上为减函数;
∵f(x)=
| 1-2x |
| 1+2x |
| 2 |
| 1+2x |
设x1<x2,f(x1)-f(x2)=
| 2 |
| 1+2x1 |
| 2 |
| 1+2x2 |
| 2(2x2-2x1) |
| (1+2x1)(1+2x2) |
∵x1<x2,
∴2x2-2x1>0,(1+2x1)(1+2x2)>0,
∴
| 2(2x2-2x1) |
| (1+2x1)(1+2x2) |
∴f(x1)-f(x2)>0,
及f(x1)>f(x2),
∴函数f(x)在R上为减函数.
(3)由(1)(2)函数为奇函数且为减函数,
∴不等式f(t2-2t)+f(-2t2+k)<0恒成立,等价为
f(t2-2t)<-f(-2t2+k)=f(2t2-k),
即t2-2t>2t2-k对t∈[-2,2],
及k>t2+2t对t∈[-2,2]恒成立,
∵y=t2+2t=(t+1)2-1在t∈[-2,2]上的最大值为8,
∴k>8,
即k的取值范围是k>8.
点评:本题主要考查函数奇偶性和单调性的判断和应用,利用函数的奇偶性和单调性将不等式转化为参数恒成立是解决本题的关键,综合性较强.

练习册系列答案
相关题目
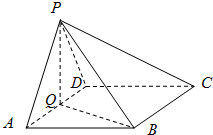 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB= 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=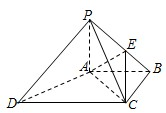 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=3,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=3,点E在棱PB上,且PE=2EB.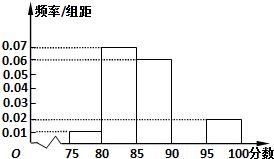 某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.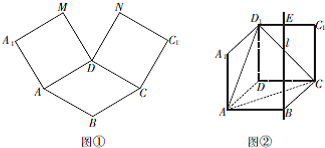 如图①,在平面内,ABCD是∠BAD=60°且AB=a的菱形,ADMA1和CDNC1都是正方形. 将两个正方形分别沿AD,CD折起,使M与N重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图②).
如图①,在平面内,ABCD是∠BAD=60°且AB=a的菱形,ADMA1和CDNC1都是正方形. 将两个正方形分别沿AD,CD折起,使M与N重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图②).