题目内容
3.(1)用分析法证明不等式:$\sqrt{6}$+$\sqrt{5}$>$\sqrt{7}$+2;(2)用综合法证明不等式:若a+b+c=1,则ab+bc+ac≤$\frac{1}{3}$.
分析 (1)将不等式两边平方寻找使不等式成立的条件即可;
(2)利用均值不等式得出a2+b2+c2≥ab+bc+ca,将a+b+c=1平方得出a2+b2+c2=1-2ab-2ac-2bc,代入a2+b2+c2≥ab+bc+ca即可得出结论.
解答 证明:(1)要证$\sqrt{6}+\sqrt{5}>\sqrt{7}+2$,
只需证${(\sqrt{6}+\sqrt{5})^2}>{(\sqrt{7}+2)^2}$.即证 $11+2\sqrt{30}>11+4\sqrt{7}$.
只需证$\sqrt{30}>2\sqrt{7}$,只需证 30>28.
而 30>28显然成立,
∴$\sqrt{6}+\sqrt{5}>\sqrt{7}+2$成立.
(2)∵a2+b2=2ab,b2+c2=2bc,c2+a2≥2ca.
∴2(a2+b2+c2 )≥2(ab+bc+ca),
∴a2+b2+c2≥ab+bc+ca.
∵a+b+c=1,∴a2+b2+c2+2ab+2bc+2ca=1
即a2+b2+c2=1-2ab-2ac-2bc,
∴1-2ab-2ac-2bc≥ab+bc+ac,
∴ab+bc+ca≤$\frac{1}{3}$.
点评 本题考查了证明方法与不等式的证明,属于中档题.

练习册系列答案
相关题目
8.△ABC中内角A,B,C的对边分别为a,b,c,若a,b,c成等比数列,且a2-c2=ac-bc,则角A的大小及$\frac{bsinB}{c}$的值分别为( )
| A. | $\frac{π}{6}$,$\frac{1}{2}$ | B. | $\frac{π}{3}$,$\frac{{\sqrt{3}}}{2}$ | C. | $\frac{π}{3}$,$\frac{1}{2}$ | D. | $\frac{π}{6}$,$\frac{{\sqrt{3}}}{2}$ |
13. 如图所示,沿田字型路线从A往N走,且只能向右或向下走,随机地选一种走法,求经过点C的概率( )
如图所示,沿田字型路线从A往N走,且只能向右或向下走,随机地选一种走法,求经过点C的概率( )
 如图所示,沿田字型路线从A往N走,且只能向右或向下走,随机地选一种走法,求经过点C的概率( )
如图所示,沿田字型路线从A往N走,且只能向右或向下走,随机地选一种走法,求经过点C的概率( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
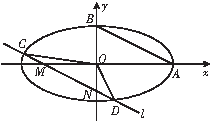 如图,A、B是离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的两个顶点,且AB=$\sqrt{5}$.
如图,A、B是离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的两个顶点,且AB=$\sqrt{5}$.