题目内容
已知函数f(x)=
的定义域是A,g(x)=2(x-4)(x+3)的定义域为B=(a,+∞),值域为(1,+∞)
(1)若不等式2x2+mx+n<0的解集是A,求m,n的值;
(2)求集合A∩(∁RB)(R为实数集)
| 1 | ||
|
(1)若不等式2x2+mx+n<0的解集是A,求m,n的值;
(2)求集合A∩(∁RB)(R为实数集)
考点:一元二次不等式的解法,函数的值域
专题:函数的性质及应用,不等式的解法及应用,集合
分析:(1)求出函数f(x)的定义域A,利用不等式与方程以及根与系数的关系,求出m、n的值;
(2)根据g(x)的定义域和值域,求出a的值,再计算B与CRB,求出A∩CRB即可.
(2)根据g(x)的定义域和值域,求出a的值,再计算B与CRB,求出A∩CRB即可.
解答:
解:(1)根据题意,得;
4-x2>0,解得-2<x<2;
∴A=(-2,2),
∴不等式2x2+mx+n<0的解集为A=(-2,2),
∴方程2x2+mx+n=0的解是-2,2,
∴-
=-2+2=0,
=-2×2=-4
即m=0,n=-8;
(2)∵g(x)=2(x-4)(x+3)的定义域为B=(a,+∞),值域为(1,+∞),
∴(x-4)(x+3)>0,
解得x>4或x<-3,
∴a=4;
∴B=(4,+∞),
∴CRB=(-∞,4];
∴A∩CRB=(-2,2)∩(-∞,4]=(-2,2).
4-x2>0,解得-2<x<2;
∴A=(-2,2),
∴不等式2x2+mx+n<0的解集为A=(-2,2),
∴方程2x2+mx+n=0的解是-2,2,
∴-
| m |
| 2 |
| n |
| 2 |
即m=0,n=-8;
(2)∵g(x)=2(x-4)(x+3)的定义域为B=(a,+∞),值域为(1,+∞),
∴(x-4)(x+3)>0,
解得x>4或x<-3,
∴a=4;
∴B=(4,+∞),
∴CRB=(-∞,4];
∴A∩CRB=(-2,2)∩(-∞,4]=(-2,2).
点评:本题考查了函数的性质与应用问题,也考查了不等式的解法与应用问题,考查了集合的基本运算问题,是综合性题目.

练习册系列答案
相关题目
不等式
>1的解集是( )
| x |
| x-1 |
| A、(-∞,0) |
| B、(1,+∞) |
| C、(0,+∞) |
| D、(0,1) |
假设某设备的使用年限x(年)和所支出的维修费用y(元)呈线性相关关系,且有如下的统计资料:
则x和y之间的线性回归方程为( )
| 使用年限x(年) | 2 | 3 | 4 | 5 | 6 |
| 维修费用y(元) | 2.2 | 3.8 | 5.5 | 6.5 | 7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 函数f(x)=sin(ωx+φ),其中ω>0,|φ|<
函数f(x)=sin(ωx+φ),其中ω>0,|φ|<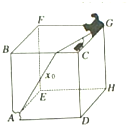 一位电脑爱好者设计了一个“猫捉老鼠”的动画游戏,如图所示,在一个边长为a的大正方体木箱的一个顶点G上,老鼠从猫的爪间逃出,沿着木箱的棱边奔向洞口,洞口子在方木箱的另一顶点A处,若老鼠在奔跑中,并不重复跳过任意一条棱边,也不再回到G点,聪明的猫也选择了一条最短的路程奔向洞口(设猫和老鼠同时从G点出发),结果猫再次在洞口A捉住了老鼠,问:
一位电脑爱好者设计了一个“猫捉老鼠”的动画游戏,如图所示,在一个边长为a的大正方体木箱的一个顶点G上,老鼠从猫的爪间逃出,沿着木箱的棱边奔向洞口,洞口子在方木箱的另一顶点A处,若老鼠在奔跑中,并不重复跳过任意一条棱边,也不再回到G点,聪明的猫也选择了一条最短的路程奔向洞口(设猫和老鼠同时从G点出发),结果猫再次在洞口A捉住了老鼠,问: