题目内容
已知函数f(x)=x3+mx2+nx+k的图象过点 P(0,3),且在点M(1,f(1))处的切线方程为6x-y=0.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若不等式f(x)≤x3+lnx+c有解,求c的取值范围.
(Ⅱ)若不等式f(x)≤x3+lnx+c有解,求c的取值范围.
考点:导数在最大值、最小值问题中的应用,函数解析式的求解及常用方法,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)函数的图象经过P点,所以把P点的坐标代入函数关系式中即可求出d的值,把d的值代入f(x)确定出函数的关系式,求出f(x)的导函数,把(1,f(1))代入导函数得到f(1)的值,又因为切线方程的斜率为6,所以得到x=1时导函数的值为6,分别列出关于m与n的两个方程,联立即可求出m与n的值,把m,n和k的值代入即可确定出f(x)的解析式.
(Ⅱ)利用函数的解析式,化简不等式,得到c的不等式,通过构造函数求出函数的最小值,即可得到c的范围.
(Ⅱ)利用函数的解析式,化简不等式,得到c的不等式,通过构造函数求出函数的最小值,即可得到c的范围.
解答:
解:(Ⅰ)由f(x)的图象经过P(0,3),知k=3,
所以f(x)=x3+mx2+nx+3,则f'(x)=3x2+2mx+n.
由在M(1,f(1))处的切线方程是6x-y=0,知6-f(1)=0,
即f(1)=6,f'(1)=6
∴
,
解得m=n=1,
故所求的解析式是f(x)=x3+x2+x+3.
(Ⅱ)不等式f(x)≤x3+lnx+c有解,
即:x3+x2+x+3≤x3+lnx+c,可得x2+x+3-lnx≤c,(x>0),
令g(x)=x2+x+3-lnx,(x>0).
g′(x)=2x+1-
=
,
令2x2+x-1=0,解得:x=
,x=-1(舍去).
x∈(0,
),g′(x)<0,g(x)是减函数,x∈(
,+∞)是增函数,
g(x)的最小值为:g(
)=
+ln2,
不等式有解,可得c≥
+ln2.
所以f(x)=x3+mx2+nx+3,则f'(x)=3x2+2mx+n.
由在M(1,f(1))处的切线方程是6x-y=0,知6-f(1)=0,
即f(1)=6,f'(1)=6
∴
|
解得m=n=1,
故所求的解析式是f(x)=x3+x2+x+3.
(Ⅱ)不等式f(x)≤x3+lnx+c有解,
即:x3+x2+x+3≤x3+lnx+c,可得x2+x+3-lnx≤c,(x>0),
令g(x)=x2+x+3-lnx,(x>0).
g′(x)=2x+1-
| 1 |
| x |
| 2x2+x-1 |
| x |
令2x2+x-1=0,解得:x=
| 1 |
| 2 |
x∈(0,
| 1 |
| 2 |
| 1 |
| 2 |
g(x)的最小值为:g(
| 1 |
| 2 |
| 19 |
| 4 |
不等式有解,可得c≥
| 19 |
| 4 |
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,会利用待定系数法求函数的解析式,函数的最值的求法,考查构造法的应用.是一道综合题.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
下列说法正确的是( )
| A、数列2,3,4与数列4,3,2是同一数列 | ||||
| B、数列1,2,3与数列1,2,3,…是同一数列 | ||||
C、1,4,2,
| ||||
| D、数列{2n-3}与-1,1,3,5,…不一定是同一数列 |
双曲线
-
=1(a>0,b>0)的两个焦点为F1,F2,若P为其图象上一点,且|PF1|=3|PF2|,则该双曲线离心率的取值范围为( )
| y2 |
| a2 |
| x2 |
| b2 |
| A、(1,2] |
| B、(1,2) |
| C、(2,+∞) |
| D、[2,+∞) |
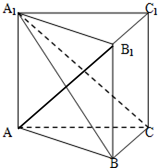 如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2.