题目内容
设
,
是两个非零向量,且
=(x1,y1),
=(x2,y2),则以下等式中与
•
=0等价的个数有( )
①
=0或
=0或
⊥
②x1x2=-y1y2③|
+
|=|
-
|④|
+
|=
.
| m |
| n |
| m |
| n |
| m |
| n |
①
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| m2+n2 |
| A、1 | B、2 | C、3 | D、4 |
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:根据题意,利用平面向量的数量积为0,判断两个非零向量互相垂直即可.
解答:
解:∵
,
是两个非零向量,∴①错误;
∵
•
=0,∴
⊥
,即x1x2+y1y2=0,∴x1x2=-y1y2,②正确;
∵
•
=0,∴(
+
)2=(
-
)2=
2+
2,
∴|
+
|=|
-
|,③正确;
∴|
+
|=
,④正确.
综上,正确的是②③④.
故选:C.
| m |
| n |
∵
| m |
| n |
| m |
| n |
∵
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
∴|
| m |
| n |
| m |
| n |
∴|
| m |
| n |
|
综上,正确的是②③④.
故选:C.
点评:本题考查了利用平面向量的数量积,判断两个非零向量互相垂直的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知命题p:3<2,命题q:3>2,则下列判断正确的是( )
| A、“¬p”为真命题 |
| B、“¬q”为真命题 |
| C、“p∨q”为假命题 |
| D、“p∧q”为真命题 |
“x>2”是“x2>4”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、既充分又必要条件 |
| D、既不充分又不必要条件 |
设Sn是等比数列{an}的前n项和,若
=3,则
=( )
| S4 |
| S2 |
| S6 |
| S4 |
| A、、2 | ||
B、
| ||
C、
| ||
| D、l或2 |
函数f(x)=
( )
| 3x-1 |
| 3x+1 |
| A、是偶函数,但不是奇函数 |
| B、是奇函数,但不是偶函数 |
| C、既是奇函数,又是偶函数 |
| D、不是奇函数,也不是偶函数 |
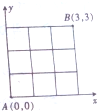 如图,电子青蛙从点A(0,0)出发,每跳一步只向上或右跳一单位长度,设每跳一步相互独立,且向上或向右的概率都为
如图,电子青蛙从点A(0,0)出发,每跳一步只向上或右跳一单位长度,设每跳一步相互独立,且向上或向右的概率都为