题目内容
已知数列{an}的前n项和是Sn,且Sn+
an=1(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log3(1-Sn+1)(n∈N*),求
+
+…+
的值.
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)设bn=log3(1-Sn+1)(n∈N*),求
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| b100b101 |
考点:数列的求和,数列递推式
专题:常规题型,等差数列与等比数列
分析:(1)由Sn+
an=1,知Sn=-
an+1.当n=1时,S1=-
a1+1,则a1=
,当n≥2时,Sn-1=-
an-1+1,故an=
an-1,由此能够求出数列{an}的通项公式an.
(2)求出1-Sn=
an=(
)n,代入bn=log3(1-sn)中得bn=-n-1,利用
=
-
,化简,问题得以解决.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
(2)求出1-Sn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
解答:
解:(1)当n=1时,a1=s1,由S1+
an=1,得a1=
,
当n≥2时,
∵Sn=1-
an,Sn-1=1-
an-1,
∴Sn-Sn-1=-
(an-an-1),
∴an=
an-1,
∴{an}是以
为首项,
为公比的等比数列.
故an=
•(
)n-1=2•(
)n.
(2)∵1-Sn=
an=(
)n,
∴bn=log3(1-Sn+1)=log3(
)n+1=-n-1
∵
=
=
-
,
∴
+
+…+
=(
-
)+(
-
)+…+(
-
)
=
-
=
.
| 1 |
| 2 |
| 2 |
| 3 |
当n≥2时,
∵Sn=1-
| 1 |
| 2 |
| 1 |
| 2 |
∴Sn-Sn-1=-
| 1 |
| 2 |
∴an=
| 1 |
| 3 |
∴{an}是以
| 2 |
| 3 |
| 1 |
| 3 |
故an=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)∵1-Sn=
| 1 |
| 2 |
| 1 |
| 3 |
∴bn=log3(1-Sn+1)=log3(
| 1 |
| 3 |
∵
| 1 |
| bnbn+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
∴
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| b100b101 |
=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 100 |
| 1 |
| 101 |
=
| 1 |
| 2 |
| 1 |
| 101 |
=
| 25 |
| 51 |
点评:考查学生灵活运用做差法求数列通项公式的能力,以及会求等比数列的通项公式及前n项和的公式.

练习册系列答案
相关题目
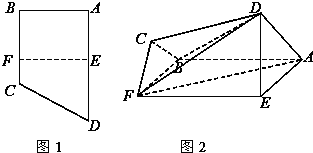 如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E、F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE.
如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E、F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE.