题目内容
2.已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,若此椭圆上存在不同的两点A,B关于直线y=4x+m对称,则实数m的取值范围是( )| A. | (-$\frac{2\sqrt{13}}{13}$,$\frac{2\sqrt{2}}{13}$) | B. | (-$\frac{2\sqrt{13}}{13}$,$\frac{2\sqrt{13}}{13}$) | C. | (-$\frac{\sqrt{2}}{13}$,$\frac{2\sqrt{13}}{13}$) | D. | (-$\frac{2\sqrt{3}}{13}$,$\frac{2\sqrt{3}}{13}$) |
分析 设椭圆上两点A(x1,y1)、B(x2,y2)关于直线y=4x+m对称,AB中点为M(x0,y0),利用平方差法与直线y=4x+m可求得x0=-m,y0=-3m,点M(x0,y0)在椭圆内部,将其坐标代入椭圆方程即可求得m的取值范围.
解答 解:椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,即:3x2+4y2-12=0,
设椭圆上两点A(x1,y1)、B(x2,y2)关于直线y=4x+m对称,AB中点为M(x0,y0),
则 3x12+4y12-12=0,①
3x22+4y22-12=0 ②
①-②得:3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,即 3•2x0•(x1-x2)+4•2y0•(y1-y2)=0,
∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{3}{4}$•$\frac{{x}_{0}}{{y}_{0}}$=-$\frac{1}{4}$.
∴y0=3x0,代入直线方程y=4x+m得x0=-m,y0=-3m;
因为(x0,y0)在椭圆内部,
∴3m2+4•(-3m)2<12,即3m2+36m2<12,解得-$\frac{2\sqrt{13}}{13}$<m<$\frac{2\sqrt{13}}{13}$.
故选:B.
点评 本题考查直线与圆锥曲线的综合问题,着重考查平方差法的应用,突出化归思想的考查,属于难题.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
12. 如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a\;,\;b>0)$的左、右两焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M.若|MF2|=|F1F2|,则C的离心率是( )
如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a\;,\;b>0)$的左、右两焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M.若|MF2|=|F1F2|,则C的离心率是( )
 如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a\;,\;b>0)$的左、右两焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M.若|MF2|=|F1F2|,则C的离心率是( )
如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a\;,\;b>0)$的左、右两焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M.若|MF2|=|F1F2|,则C的离心率是( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
13.复数$\frac{2i}{1-i}$等于( )
| A. | -2+2i | B. | 1+i | C. | -1+i | D. | 2-2i |
7.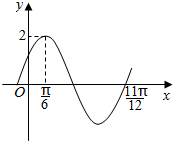 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )
 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )| A. | f(x)=2sin(x+$\frac{π}{3}$) | B. | f(x)=2sin(2x+$\frac{π}{6}$) | C. | f(x)=2sin(2x-$\frac{π}{6}$) | D. | f(x)=2sin(4x-$\frac{π}{6}$) |
11.空间直角坐标系xOy中,x轴上的一点M到点A(1,-3,1)与点B(2,0,2)的距离相等,则点M的坐标( )
| A. | (-$\frac{3}{2}$,0,0) | B. | (3,0,0) | C. | ($\frac{3}{2}$,0,0) | D. | (0,-3,0) |
12.命题p:函数y=log2($\sqrt{{x}^{2}+1}-x$)是奇函数,命题q:“对函数f(x),若f′(x0)=0,则x=x0为函数的极值点”.则下列命题中真命题是( )
| A. | p∧q | B. | p∨q | C. | (¬p)∧q | D. | (¬p)∧(¬q) |