题目内容
10.已知cos(θ+$\frac{π}{4}$)=-$\frac{\sqrt{10}}{10}$,θ∈(0,$\frac{π}{2}$),求sin(2θ-$\frac{π}{3}$)的值.分析 由二倍角公式和同角三角函数基本关系可得cos2θ和sin2θ,代入sin(2θ-$\frac{π}{3}$)=$\frac{1}{2}$sin2θ-$\frac{\sqrt{3}}{2}$cos2θ,计算可得.
解答 $\frac{1}{2}×\frac{4}{5}-\frac{\sqrt{3}}{2}×(-\frac{3}{5})=\frac{4+3\sqrt{3}}{10}$
点评 本题考查两角和与差的三角函数公式,涉及二倍角公式和同角三角函数基本关系,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知loga2=m,loga3=n,则a2m+n=( )
| A. | 6 | B. | 7 | C. | 11 | D. | 12 |
2.已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,若此椭圆上存在不同的两点A,B关于直线y=4x+m对称,则实数m的取值范围是( )
| A. | (-$\frac{2\sqrt{13}}{13}$,$\frac{2\sqrt{2}}{13}$) | B. | (-$\frac{2\sqrt{13}}{13}$,$\frac{2\sqrt{13}}{13}$) | C. | (-$\frac{\sqrt{2}}{13}$,$\frac{2\sqrt{13}}{13}$) | D. | (-$\frac{2\sqrt{3}}{13}$,$\frac{2\sqrt{3}}{13}$) |
20.若复数z满足zi=-1-i,则在复平面内,z所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
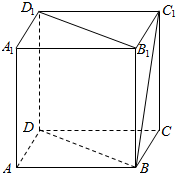 如图,正方体ABCD-A1B1C1D1中,直线BC1和B1D1所成角的大小为60°;直线BC1和平面B1D1DB所成角的大小为30°.
如图,正方体ABCD-A1B1C1D1中,直线BC1和B1D1所成角的大小为60°;直线BC1和平面B1D1DB所成角的大小为30°. 交通部门对某路段公路上行驶的汽车速度实施监控,从速度在50-90km/h的汽车中抽取150辆进行分析,得到数据的频率分布直方图如图所示,则速度在70km/h以下的汽车有75辆.
交通部门对某路段公路上行驶的汽车速度实施监控,从速度在50-90km/h的汽车中抽取150辆进行分析,得到数据的频率分布直方图如图所示,则速度在70km/h以下的汽车有75辆.