题目内容

计算
∫
2
0
f（x）dx，其中f（x）=
2x，0≤x＜1
x+1，1≤x≤2
．
考点：定积分
专题：导数的概念及应用
分析：根据定义，分两部分直接计算即可．
解答： 解：
∫
2
0
f（x）dx=
∫
1
0
2xdx+
∫
2
1
(x+1)dx
=
∫
1
0
x2dx+
∫
2
1
d(
1
2
x2+x)
=（1-0）+（
1
2
×22+2-
1
2
-1）=
7
2
．
点评：本题考查定积分的计算，属基础题．
练习册系列答案
相关题目
设函数f（x）=6lnx+ax2-10ax+25a，其中a∈R，曲线y=f（x）在点（1，f（1））处的切线与y轴相交于点（0，6）．
（1）求a的值；
（2）求函数f（x）的单调区间与极值．
已知AD，CE分别是△ABC的边BC，AB的中线，且
AD
=
a
，
CE
=
b
，则
AC
=
 
（用
a
，
b
表示）
定义在实数集R上奇函数f（x）的最小正周期为20，在区间（0，10）内方程f（x）=0有且仅有一个解x=3，则方程f（
x
4
+3）=0在[-100，400]上不同的解的个数为（　　）
A、20B、25C、26D、27
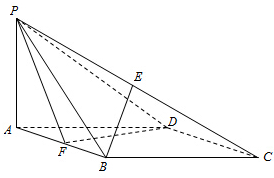如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠BAD=60°，AB=2，PA=1，PA⊥平面ABCD，E是PC的中点，F是AB的中点．
（Ⅰ） 求证：BE∥平面PDF；
（Ⅱ）求证：平面PDF⊥平面PAB；
（Ⅲ）求平面PAB与平面PCD所成的锐二面角的大小．
已知sinx=
2
3
，cosy=-
3
4
，且x、y都是第二象限角，求sin（x+y）及sin（x-y）的值．
在（0，2π）上满足
tan2x
=-tanx的x的取值范围是
 
．
在△ABC中，已知a2+b2=2010c2，求证：
2sinAsinBcosC
sin2(A+B)
为定值．
如图，半径都为1的三个圆两两相交，
AB
，
BC
，
AC
的长度相等，
CD
的长度为
π
2
，在图中任一圆内任取一点，则此点取自阴影部分的概率为（　　）
A、
12π
7π+2
3
+6
B、
8π
7π+2
3
+6
C、
10π
7π+2
3
+6
D、
6π+12
7π+2
3
+6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网