题目内容
为了参加冬季运动会的5000m长跑比赛,某同学给自己定制了7天的训练计划;第1天跑5000m.以后每天比前一天多跑500m,这个同学7天一共将跑多长的距离?
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由题意和等差数列的定义判断出:这个同学每天跑的距离构成一个等差数列,利用等差数列的前n项和公式求出这个同学7天一共跑距离.
解答:
解:由题意可得,
这个同学每天跑的距离构成一个等差数列,且首项为5000,公差是500,
所以这个同学7天一共跑的距离S=7×5000+
×500=45500(m),
答:这个同学7天一共将跑45500m.
这个同学每天跑的距离构成一个等差数列,且首项为5000,公差是500,
所以这个同学7天一共跑的距离S=7×5000+
| 7×6 |
| 2 |
答:这个同学7天一共将跑45500m.
点评:本题考查等差数列的实际应用,以及等差数列的定义、前n项和公式,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=
sin2xsinφ+cos2xcosφ-
sin(
+φ)(0<φ<π),将凼数f(x)的图象向左移
个单位后关于y轴对称,则φ等于( )
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,半径都为1的三个圆两两相交,
如图,半径都为1的三个圆两两相交, |
| AB |
 |
| BC |
 |
| AC |
 |
| CD |
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=
,则函数g(x)=f(x)-x在区间[-5,5]上的零点之和为( )
|
| A、15 | B、16 | C、30 | D、32 |
| cos200 |
| sin200 |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
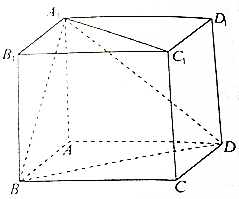 如图,正方体ABCD-A1B1C1D1的棱长为a,求:
如图,正方体ABCD-A1B1C1D1的棱长为a,求: