题目内容
设直线l方程为（m+1）x+y+（2-m）=0，证明：l恒过第四象限．
考点：恒过定点的直线
专题：计算题,直线与圆
分析：确定直线恒通过定点（1，-3），即可证明l恒过第四象限．
解答：
证明：由（m+1）x+y+（2-m）=0，可得（x-1）m+x+y+2=0
令x-1=0，x+y+2=0
∴x=1，y=-3
∴直线恒通过定点（1，-3），
∵点（1，-3）在第四象限，
∴l恒过第四象限．
令x-1=0，x+y+2=0
∴x=1，y=-3
∴直线恒通过定点（1，-3），
∵点（1，-3）在第四象限，
∴l恒过第四象限．
点评：本题考查直线恒通过定点，考查学生的计算能力，确定直线恒通过定点是关键．
练习册系列答案
相关题目
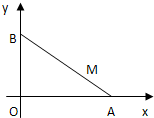如图，长为m+1（m＞0）的线段AB的两个端点A和B分别在x轴和y轴上滑动，点M是线段AB上的一点，且