题目内容
从6名教师中选4名开发A、B、C、D四门课程，要求每门课程有一名教师开发，每名教师只开发一门课程，且这6名中甲、乙两人不开发A课程，则不同的选择方案共有（ ）
| A、300种 | B、240种 |
| C、144种 | D、96种 |
考点：排列、组合的实际应用
专题：计算题
分析：根据题意，按甲乙是否参加分3种情况讨论：①、选出的4人不含甲乙，②、选出的4人只含甲、乙中的一人，③、选出的4人含甲、乙二人，甲乙均参加，由排列、组合公式分别求出每种情况下的选择方案数目，由分类计数原理将其相加即可得答案．
解答：
解：根据题意，需要从6名教师中选4名，按甲乙是否参加分3种情况讨论：
①、选出的4人不含甲乙，将剩余的4人全排列，对应四门课程即可，有A44=24种选择方案，
②、选出的4人只含甲、乙中的一人，
甲或乙参加有2种情况，在剩余4人中选出三人，有C43=4种选法，
此时甲有3门课程可选，剩余3人全排列，对应其他三门课程即可，共有3A33=18种方案，
此时有2×4×18=144种选择方案，
③、选出的4人含甲、乙二人，甲乙均参加，有1种情况，
在剩余4人中选出2人，有C42=6种选法，
此时甲、乙有A32=6种情况，剩余2人全排列，对应其他二门课程即可，共有6A22=12种方案，
此时有1×6×12=72种选择方案，
共有24+144+72=240种选择方案；
故答案为：B．
①、选出的4人不含甲乙，将剩余的4人全排列，对应四门课程即可，有A44=24种选择方案，
②、选出的4人只含甲、乙中的一人，
甲或乙参加有2种情况，在剩余4人中选出三人，有C43=4种选法，
此时甲有3门课程可选，剩余3人全排列，对应其他三门课程即可，共有3A33=18种方案，
此时有2×4×18=144种选择方案，
③、选出的4人含甲、乙二人，甲乙均参加，有1种情况，
在剩余4人中选出2人，有C42=6种选法，
此时甲、乙有A32=6种情况，剩余2人全排列，对应其他二门课程即可，共有6A22=12种方案，
此时有1×6×12=72种选择方案，
共有24+144+72=240种选择方案；
故答案为：B．
点评：本题考查排列、组合的应用，涉及分类加法原理，分类讨论的关键在于确定分类讨论的依据、标准，一定做到不重不漏．
练习册系列答案
相关题目
在复平面内，复数1+i对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
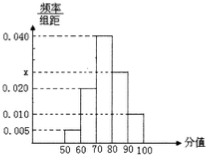为了全面推进素质教育，教育部门对某省500所中小学进行调研考评，考评分数在80分以上（含80分）的授予“素质教育先进学校”称号，考评统计结果如图的频率分布直方图所示，则应授予“素质教育先进学校”称号的学校有（ ）所．| A、125 | B、175 |
| C、325 | D、50 |
若sinα＜0，且tanα＜0，则α是（ ）的角．
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知命题p：?x∈R，x+
≥2，命题q：?x∈R，sinx+cosx=
，下列结论正确的是（ ）
| 1 |
| x |
| 2 |
| A、命题“p∧q”是真命题 |
| B、命题“（￢p）∧q”是真命题 |
| C、命题“（￢p）∨q”是假命题 |
| D、命题“（￢p）∨（￢q）”是假命题 |
某程序框图如图所示，则该程序运行后输出的值为（ ）
| A、23 | B、47 | C、95 | D、191 |
若命题“?（p∧q）”为真命题，则（ ）
| A、p、q均为真命题 |
| B、p、q中至少有一个为真命题 |
| C、p、q中至多有一个为真命题 |
| D、p、q均为假命题 |