题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c,向量
=(tanA+tanC,
),
=(tanAtanC-1,1),且
∥
.
(1)求角B;
(2)若b=2,求△ABC的面积的最大值.
| m |
| 3 |
| n |
| m |
| n |
(1)求角B;
(2)若b=2,求△ABC的面积的最大值.
考点:正弦定理,基本不等式
专题:解三角形
分析:(1)通过两向量平行,求得tanA和tanC的关系,求得tanB,进而求得B.
(2)利用余弦定理求得a和c的关系式,利用基本不等式的性质求得ac的最大值,进而利用三角形面积公式求得其最大值.
(2)利用余弦定理求得a和c的关系式,利用基本不等式的性质求得ac的最大值,进而利用三角形面积公式求得其最大值.
解答:
解:(1)∵m∥n,
∴tanA+tanC=
(tanAtanC-1),
∴
=-
,即tan(A+C)=-
,
∴tanB=-tan(A+C)=
,
∵B∈(0,π),
∴B=
.
(2)在△ABC中,由余弦定理有,cosB=
=
,
∴a2+c2=ac+4,
∵a2+c2≥2ac,
∴ac≤4,当且仅当a=c=2时,取等,
∴△ABC的面积S=
acsinB≤
×4=
,
故△ABC的面积的最大值为
.
∴tanA+tanC=
| 3 |
∴
| tanA+tanC |
| 1-tanAtanC |
| 3 |
| 3 |
∴tanB=-tan(A+C)=
| 3 |
∵B∈(0,π),
∴B=
| π |
| 3 |
(2)在△ABC中,由余弦定理有,cosB=
| a2+c2-b2 |
| 2ac |
| 1 |
| 2 |
∴a2+c2=ac+4,
∵a2+c2≥2ac,
∴ac≤4,当且仅当a=c=2时,取等,
∴△ABC的面积S=
| 1 |
| 2 |
| ||
| 4 |
| 3 |
故△ABC的面积的最大值为
| 3 |
点评:本题主要考查了余弦定理的运用,向量数量积,基本不等式的基本性质.考查了学生推理和运算的能力.

练习册系列答案
相关题目
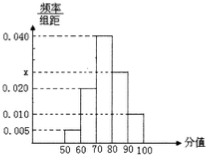 为了全面推进素质教育,教育部门对某省500所中小学进行调研考评,考评分数在80分以上(含80分)的授予“素质教育先进学校”称号,考评统计结果如图的频率分布直方图所示,则应授予“素质教育先进学校”称号的学校有( )所.
为了全面推进素质教育,教育部门对某省500所中小学进行调研考评,考评分数在80分以上(含80分)的授予“素质教育先进学校”称号,考评统计结果如图的频率分布直方图所示,则应授予“素质教育先进学校”称号的学校有( )所.| A、125 | B、175 |
| C、325 | D、50 |
若命题“?(p∧q)”为真命题,则( )
| A、p、q均为真命题 |
| B、p、q中至少有一个为真命题 |
| C、p、q中至多有一个为真命题 |
| D、p、q均为假命题 |
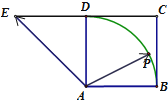 如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量
如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量