题目内容
如图所示是一几何体的三视图,则该几何体的表面积为( )


| A、2 | ||||
B、
| ||||
C、4+
| ||||
D、4+
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:几何体为三棱锥,且三棱锥的一条侧棱垂直于底面,高为1,三棱锥的底面为直角边长为2的等腰直角三角形,结合其直观图求得AB长及侧面△SAB的斜高,计算各面的面积和可得答案.
解答:
解:由三视图知:几何体为三棱锥,且三棱锥的一条侧棱垂直于底面,高为1,
三棱锥的底面为直角边长为2的等腰直角三角形,如图:

D为底面直角三角形斜边上的中点,∴SD⊥AB,SD=
=
,AB=2
.
∴几何体的表面积S=2×
×2×1+
×2×2+
×2
×
=4+
.
故选:D.
三棱锥的底面为直角边长为2的等腰直角三角形,如图:

D为底面直角三角形斜边上的中点,∴SD⊥AB,SD=
| 1+2 |
| 3 |
| 2 |
∴几何体的表面积S=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
故选:D.
点评:本题考查了由三视图求几何体的表面积,根据三视图判断几何体的结构特征是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在复平面内,复数1+i对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合M={x|
>0},N={x|3x+2>0},则M∩N=( )
| x-3 |
| x+1 |
| A、(-∞,-1) | ||
B、(-1,-
| ||
C、(-
| ||
| D、(3,+∞) |
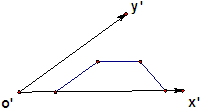 一个水平放置的平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则该平面图形的面积等于( )
一个水平放置的平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则该平面图形的面积等于( )A、
| ||||||
B、1+
| ||||||
C、1+
| ||||||
D、2+
|
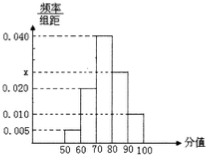 为了全面推进素质教育,教育部门对某省500所中小学进行调研考评,考评分数在80分以上(含80分)的授予“素质教育先进学校”称号,考评统计结果如图的频率分布直方图所示,则应授予“素质教育先进学校”称号的学校有( )所.
为了全面推进素质教育,教育部门对某省500所中小学进行调研考评,考评分数在80分以上(含80分)的授予“素质教育先进学校”称号,考评统计结果如图的频率分布直方图所示,则应授予“素质教育先进学校”称号的学校有( )所.| A、125 | B、175 |
| C、325 | D、50 |
若sinα<0,且tanα<0,则α是( )的角.
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |