题目内容
已知复数z1=-1+2i,z2=1-i,z3=3-4i,它们在复平面上对应的点分别为A,B,C,
=λ
+μ
(λ,μ∈R),则μ-λ的值是 .
| OC |
| OA |
| OB |
考点:复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:利用复数的几何意义,结合向量的基本定理,建立方程关系即可得到结论.
解答:
解:复数z1=-1+2i,z2=1-i,z3=3-4i,它们在复平面上对应的点分别为A(-1,2),B(1,-1),C(3,-4),
由
=λ
+μ
得(3,-4)=λ(-1,2)+μ(1,-1)=(-λ+μ,2λ-μ),
即
,
解得
,
则μ-λ=2-(-1)=2+1=3,
故答案为:3
由
| OC |
| OA |
| OB |
即
|
解得
|
则μ-λ=2-(-1)=2+1=3,
故答案为:3
点评:本题主要考查复数的几何意义,以及向量的基本定理,建立方程组是解决本题的关键.

练习册系列答案
相关题目
执行如图所示的程序框图.若输入a=3,则输出i的值是( )


| A、2 | B、3 | C、4 | D、5 |
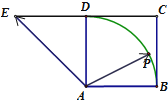 如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量
如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量