题目内容
2.在△ABC中,若sin2(B+C)+cos2B+cos2C+sinBsinC≥2,则角A的取值范围是( )| A. | $(0,\frac{π}{6}]$ | B. | $[\frac{π}{3},\frac{π}{2}]$ | C. | $(0,\frac{π}{3}]$ | D. | $[\frac{π}{3},π)$ |
分析 先利用正弦定理把不等式中正弦的值转化成边,进而代入到余弦定理公式中求得cosA的范围,进而求得A的范围.
解答 解:sin2(B+C)+cos2B+cos2C+sinBsinC≥2⇒sin2A≤sin2B+sin2C-sinBsinC,
由正弦定理可知a=2RsinA,b=2RsinB,c=2RsinC,
∵sin2A≤sin2B+sin2C-sinBsinC,
∴a2≤b2+c2-bc,
∴bc≤b2+c2-a2
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$≥$\frac{1}{2}$,
∴A≤$\frac{π}{3}$,
∵A>0,
∴A的取值范围是(0,$\frac{π}{3}$]
故选:C.
点评 本题主要考查了正弦定理和余弦定理的应用.作为解三角形中常用的两个定理,考生应能熟练记忆.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
12.已知a≥0,函数f (x)=(x2-2ax)ex,若f (x)在[-1,1]上是单调减函数,则a的取值范围是( )
| A. | (0,$\frac{3}{4}$) | B. | ($\frac{1}{2}$,$\frac{3}{4}$) | C. | (0,$\frac{1}{2}$) | D. | [$\frac{3}{4}$,+∞) |
13.直线l在平面α内,直线m平行于平面α,且与直线l异面,动点P在平面α上,且到直线l、m距离相等,则点P的轨迹为( )
| A. | 直线 | B. | 椭圆 | C. | 抛物线 | D. | 双曲线 |
10.若O为坐标原点,已知实数x,y满足条件$\left\{\begin{array}{l}x+y≥1\\ x-y≥-1\\ 2x-y≤2\end{array}\right.$,在可行域内任取一点P(x,y),则|OP|的最小值为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{3}{2}$ |
7.复数z=|$\sqrt{3}$-i|+i2017(i为虚数单位),则复数z为( )
| A. | 2-i | B. | 2+i | C. | 4-i | D. | 4+i |
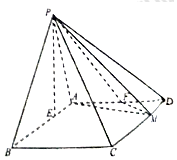 在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,$AD=2\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.
在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,$AD=2\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.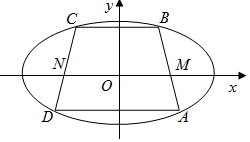 如图,已知中心在原点,焦点在x轴上的椭圆经过等腰梯形ABCD的四个顶点,两腰与x轴相交于点M,N,且$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$
如图,已知中心在原点,焦点在x轴上的椭圆经过等腰梯形ABCD的四个顶点,两腰与x轴相交于点M,N,且$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$