Question

已知g（2x+1）=x²+1，求g（x），并求使方程g（|x|）=m有4个不同的根的m取值范围．

Answer 1

考点：根的存在性及根的个数判断

专题：函数的性质及应用

分析：先求出g（x）的表达式，从而求出g（|x|）的表达式，将问题转化为函数的交点问题，画出图象即可求出答案．

解答： 解：令t=2x+1，⇒x=

t-1

2

，
g（t）=

1

4

（t²-2t+5），
∴g（x）=

1

4

（x²-2x+5），∴
g（|x|）=

1

4

（|x|²-2|x|+5）
=

1 4 (x2-2x+5)，x≥0 1 4 (x2+2x+5)，x＜0

=

1 4 (x-1)2+1，x≥0 1 4 (x+1)2+1，x＜0

，
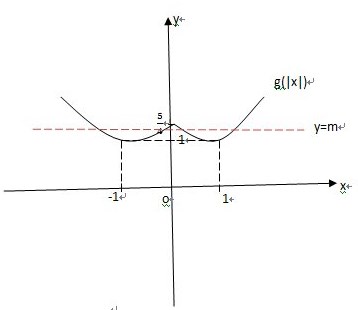绘图：如图示：
g（|x|）=m有4个不同的根等价于直线y=m与曲线g（|x|）有四个不同交点]，
∴m∈（1，

5

4

）．．

点评：本题考查了函数解析式的求法，考查函数的零点问题，考查转化思想，数形结合思想，是一道中档题．