题目内容
已知f(x)为一次函数,g(x)为二次函数,且f[g(x)]=g[f(x)],求f(x)的解析式.
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:由于f(x)为一次函数,g(x)为二次函数,可设f(x)=mx+n,g(x)=ax2+bx+c,m,a≠0.由于f[g(x)]=g[f(x)],可得m(ax2+bx+c)+n=a(mx+n)2+b(mx+n)+c,化为(ma-am2)x2+(mb-2amn-bm)x+mc-an2-bn-c=0,得到
,解得m,n即可.
|
解答:
解:∵f(x)为一次函数,g(x)为二次函数,
设f(x)=mx+n,g(x)=ax2+bx+c,m,a≠0.
∵f[g(x)]=g[f(x)],
∴m(ax2+bx+c)+n=a(mx+n)2+b(mx+n)+c,
化为(ma-am2)x2+(mb-2amn-bm)x+mc-an2-bn-c=0,
∴
,解得m=1,n=0.
∴f(x)=x.
设f(x)=mx+n,g(x)=ax2+bx+c,m,a≠0.
∵f[g(x)]=g[f(x)],
∴m(ax2+bx+c)+n=a(mx+n)2+b(mx+n)+c,
化为(ma-am2)x2+(mb-2amn-bm)x+mc-an2-bn-c=0,
∴
|
∴f(x)=x.
点评:本题考查了一次函数、二次函数的解析式、恒等式问题,考查了计算能力,属于中档题.

练习册系列答案
相关题目
如图,正方体ABCD-A1B1C1D1中,直线AB1与BC1所成角为( )


| A、30° | B、45° |
| C、60° | D、90° |
在正三棱柱中,AB=AA1=1,P在平面ABC内运动,使得三角形AC1P的面积为
,则动点P的轨迹是( )
| 1 |
| 2 |
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
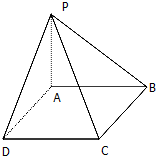 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=