题目内容
10.已知函数f(x)=ex-m-ln2x(Ⅰ)若m=1,求函数f(x)的极小值;
(Ⅱ)设m≤2,证明:f(x)+ln2>0.
分析 (Ⅰ)求出f′(x),f″(x),得到f′(x)的单调性,从而求出f(x)的单调区间,得到f(x)的极小值即可;
(Ⅱ)x∈(0,+∞)时,ex-m≥ex-2≥x-1恒成立,取函数h(x)=x-1-ln(2x)(x>0),可得f(x)=ex-m-ln(2x)≥ex-2-ln(2x)≥x-1-ln(2x)≥-ln2,即可得出结论.
解答 (Ⅰ)解:函数f(x)的定义域是(0,+∞),
m=1时:f(x)=ex-1-ln(2x),
∴f′(x)=ex-1-$\frac{1}{x}$,f″(x)=ex-1+$\frac{1}{{x}^{2}}$>0,
故f′(x)在(0,+∞)递增,而f′(1)=0,
∴x=1是f′(x)=0的唯一零点,
因此,当x∈(0,1)时,f′(x)<0,f(x)递减,
x∈(1,+∞)时,f′(x)>0,f(x)递增,
∴函数f(x) 在(0,1)上单调递减,在(1,+∞)上单调递增,
∴f(x)的极小值是f(1)=1-ln2;
(Ⅱ)证明:当m≤2,x∈(0,+∞)时,ex-m≥ex-2,
又ex≥x+1,∴ex-m≥ex-2≥x-1,
取函数h(x)=x-1-ln(2x)(x>0),h′(x)=1-$\frac{1}{x}$,
当0<x<1时,h′(x)<0,h(x)单调递减;
当x>1时,h′(x)>0,h(x)单调递增,
得函数h(x)在x=1时取唯一的极小值即最小值为h(1)=-ln2,
∴f(x)=ex-m-ln(2x)≥ex-2-ln(2x)≥x-1-ln(2x)≥-ln2,
而上式三个不等号不能同时成立,故f(x)+ln2>0.
点评 本题考查利用导数研究函数的极值、单调性,考查学生灵活运用知识分析解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列函数是偶函数,且在[0,1]上单调递增的是( )
| A. | y=sin(x+$\frac{π}{2}$) | B. | y=-cos4x | C. | y=-x2 | D. | y=|sin(π+x)| |
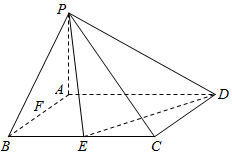 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2AB,E,F是线段BC,AB的中点.
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2AB,E,F是线段BC,AB的中点.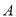 型和20台
型和20台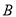 型电脑的利润为4000元,销售20台
型电脑的利润为4000元,销售20台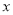 台,这100台电脑的销售总利润为
台,这100台电脑的销售总利润为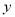 元.
元.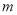 (
(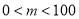 )元,且限定商店最多购进
)元,且限定商店最多购进