题目内容
16．已知△ABC中，$\frac{AC}{BC}$=$\frac{3}{2}$，B=60°，则sinA=$\frac{\sqrt{3}}{3}$．分析 利用正弦定理，代入计算可得结论．
解答 解：∵△ABC中，$\frac{AC}{BC}$=$\frac{3}{2}$，B=60°，
∴$\frac{sin60°}{sinA}$=$\frac{3}{2}$，
∴sinA=$\frac{\sqrt{3}}{3}$，
故答案为：$\frac{\sqrt{3}}{3}$．
点评 本题考查正弦定理，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
6．已知命题p：?m∈R，使得函数f（x）=x3+（m-1）x2-2是奇函数，命题q：向量$\overrightarrow{a}$=（x1，y1），$\overrightarrow{b}$=（x2，y2），则“$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$”是：“$\overrightarrow{a}$∥$\overrightarrow{b}$”的充要条件，则下列命题为真命题的是（ ）
| A． | p∧q | B． | （￢p）∧q | C． | p∧（￢q） | D． | （￢p）∧（￢q） |
7．已知集合A={x|x2-4x+3＜0}，B={x|2＜x＜4}，则A∩B=（ ）
| A． | （1，3） | B． | （1，4） | C． | （2，3） | D． | （2，4） |
11．函数f（x）=sin（x+$\frac{π}{3}$）+sin（x-$\frac{π}{3}$）的最大值是（ ）
| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | $\sqrt{3}$ |
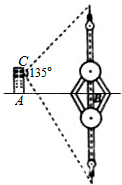如图所示，某人居住在离地面100米处的楼房C处，测得平静江河的对面转播塔尖以及转播塔的倒影中的塔尖的张角为135°，又知楼房离转播塔的距离AB=200m，试问：能否推算出转播塔的高度？若能，请确定塔高；若不能，请说明理由．
是非零向量且满足
则
的夹角是（ ） 
B.
C.
D.
12．Rt△ABC中，斜边BC为4，以BC中点为圆心，作半径为1的圆，分别交BC于P、Q两点，则|AP|2+|AQ|2+|PQ|2的值为（ ）
| A． | 4+$\sqrt{17}$ | B． | 3+$2\sqrt{5}$ | C． | $\frac{19}{2}$ | D． | 14 |