题目内容
4.若sin4α+cos4α=$\frac{5}{9}$,且α是第二象限角,则sin2α=-$\frac{2\sqrt{2}}{3}$.分析 利用完全平方公式求出sin2αcos2α的值,再根据α的象限得出sinαcosα的值,代入二倍角公式得出sin2α.
解答 解:∵sin4α+cos4α=(sin2α+cos2α)2-2sin2αcos2α=1-2sin2αcos2α=$\frac{5}{9}$,
∴sin2αcos2α=$\frac{2}{9}$.
∵α是第二象限角,∴sinαcosα=-$\frac{\sqrt{2}}{3}$.
∴sin2α=2sinαcosα=-$\frac{2\sqrt{2}}{3}$.
故答案为:-$\frac{2\sqrt{2}}{3}$.
点评 本题考查了同角三角函数的关系,二倍角的正弦公式,属于基础题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
14.若非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\frac{\sqrt{2}}{2}$|$\overrightarrow{b}$|,且($\overrightarrow{a}$-$\overrightarrow{b}$)⊥(3$\overrightarrow{a}$+2$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
15.如图,用5种不同的颜色涂这些正方形,让每个正方形都涂上一种颜色,且相邻的正方形的颜色不同,若颜色可反复使用,则不同的涂色方法有( )


| A. | 120种 | B. | 240种 | C. | 320种 | D. | 625种 |
 ,应用秦九韶算法计算
,应用秦九韶算法计算 时的值时,
时的值时, =_____
=_____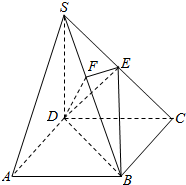 如图,在四棱锥S-ABCD中,底面ABCD是矩形,SD=DC=2AD,侧棱SD⊥底面ABCD,点E是SC的中点,点F在SB上,且EF⊥SB.
如图,在四棱锥S-ABCD中,底面ABCD是矩形,SD=DC=2AD,侧棱SD⊥底面ABCD,点E是SC的中点,点F在SB上,且EF⊥SB.